How to Compute the UV Index

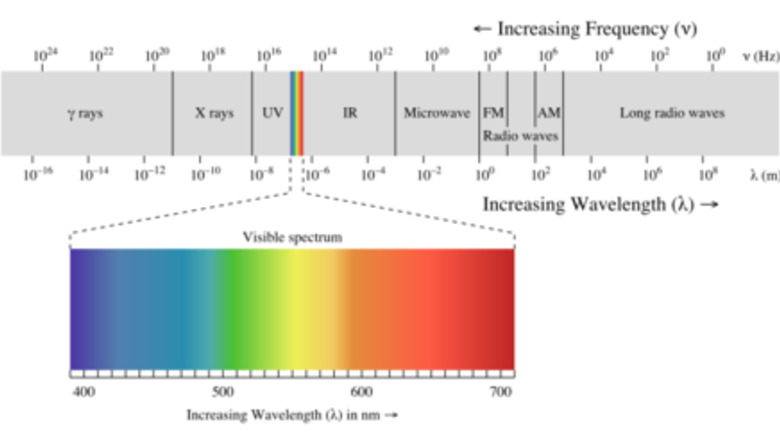
Begin with initial data that is captured by two National Oceanic and Atmospheric Administration (NOAA) satellites. This data includes global ozone levels that help forecasters determine the levels of ozone they think will exist 24 hours later. With this data, computer models use the forecast and how the sunlight will be angled, to calculate UV strength. When calculating how strong the UV radiation is, scientists only focus on the range of wavelengths from 280 nm to 400 nm. 280 nm to 400 nm are used since this range of UV passes through the ozone (the picture below shows the full range of UV light on the electromagnetic spectrum).

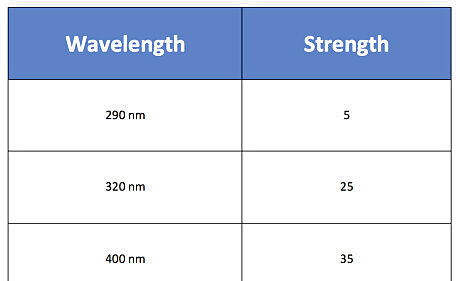
Use this preliminary data to assign value to wavelength for calculating. In a classroom setting where this calculation is occurring, this initial data would be made up unless there is access to NOAA satellite information. The made up values could be made accurate knowing the fact that the ozone absorbs longer wavelengths less than shorter wavelengths, so how intense UV is when it hits the Earth's surface is depends on wavelength. Hypothetical values shown below may not be exactly identical to how the NWS calculates UV Index, but having the strength weighted with a smaller value for shorter wavelengths is accurate. Shorter wavelengths are absorbed by the ozone more than longer wavelengths, so their strength near the Earth's surface is weaker. Follow a similar trend as in the chart below when you are working on your problem.

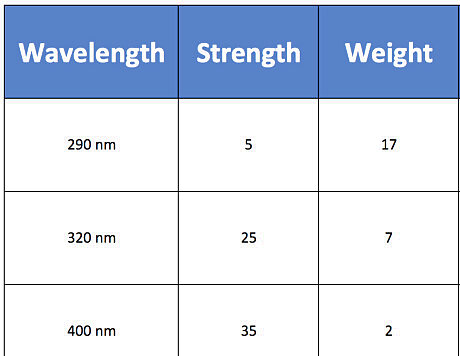
Use more initial values for how the skin of humans reacts to UV radiation. When the UV Index scale was invented, tests were done on human skin at each UV wavelength to see the effects. Scientists found that shorter wavelengths were more dangerous (shorter wavelengths have more energy). To include this information in the calculation, weighting the UV strength at different wavelengths is required. This is done using the McKinlay-Diffey erythema action spectrum (see bottom of instructions for more information on this). When doing your own problem, weight wavelengths in an opposite fashion as the strength values given earlier. Shorter wavelengths have a higher weight (more dangerous), but a lower strength factor (since they are absorbed more by the ozone) as shown in the table below. Again these values are theoretical, but they are weighted in an accurate fashion.

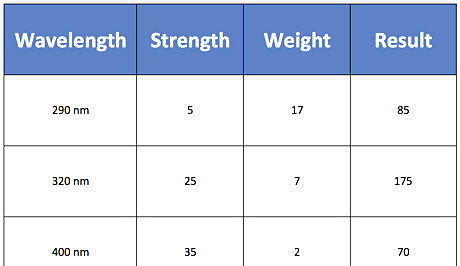
Multiply the strength of UV by the weight. Use your calculator to multiply weight and strength of the wavelength in question, and the result will be the UV radiation's direct strength at the corresponding wavelengths. Continuing with the example above, the table below gives hypothetical weighting factors for the response of skin at UV wavelengths.

Sum effective UV strength at each wavelength. As established by the inventors of the UV Index, the strength of UV at each wavelength from 290 to 400 nm is summed to represent the overall impact UV radiation has on human skin. Sticking with the example shown above, the total effect of UV is 330 (85 + 175 + 70 = 330).

Account for how clouds and elevation interfere with UV. It has been determined that for each kilometer above sea level, there is a 6% increase in the magnitude of UV (so in the calculation, you will add 0.06 for every kilometer increase). It is also known that UV radiation is absorbed by clouds, which reduces the intensity of UV that hits Earth's surface. According to the EPA: 100% of UV transmits when no clouds are present. 89% is transmitted when clouds are spotty. 73% is transmitted through broken clouds. 31% is transmitted when it is completely overcast.

Choose the scenario. To continue the example we are doing, lets choose an elevation of 5 kilometers (which is the elevation of La Rinconada, Peru - one of the highest cities in the world) and say that scattered clouds are present. The true effect of UV would have to be adjusted 30% for elevation (6% multiplied by 5 kilometers) and 89% for the scattered clouds. You then multiply the total UV effect calculated earlier by the elevation and cloud adjustment. This calculation would look like the following: 330 x 1.30 x 0.89 = 381.81 (again, a 30% increase due to elevation would be multiplied as 1.3 and not 0.3, since UV strength is increasing).

Finish the calculation. To end the calculation, you have to divide the value of UV from the step above by the number 25 (this is another part determined by the inventors of the UV Index), and round to the number you find to the closest whole number. According to the EPA, the calculation results a number between 0 and 15 or so.You have now calculated the UV Index! For the scenario we decided, the UV Index would be: 381.81 / 25 = 15.27, which rounds to 15.

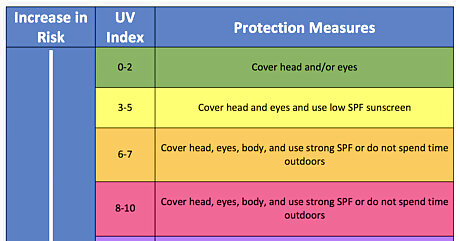
Apply the scale. From the calculated value, read a UV Index scale and adhere to the warnings associated with the value (yikes, 15 is very dangerous)!