
views
Multiplying by the Reciprocal

Convert the whole number to a fraction. To do this, make the whole number the numerator of a fraction. Make the denominator 1. For example, if you are calculating 7 ÷ 3 4 {\displaystyle 7\div {\frac {3}{4}}} 7\div {\frac {3}{4}}, you would first change 7 {\displaystyle 7} 7 to 7 1 {\displaystyle {\frac {7}{1}}} {\frac {7}{1}}.

Find the reciprocal of the divisor. The reciprocal of a number is the inverse of the number. To find the reciprocal of a fraction, reverse the numerator and denominator. For example, the inverse of 3 4 {\displaystyle {\frac {3}{4}}} {\frac {3}{4}} is 4 3 {\displaystyle {\frac {4}{3}}} {\frac {4}{3}}.

Multiply the two fractions. To multiply fractions, first multiply the numerators together. Then, multiply the denominators together. The product of the two fractions equals the quotient of your original division problem. For example, 7 1 × 4 3 = 28 3 {\displaystyle {\frac {7}{1}}\times {\frac {4}{3}}={\frac {28}{3}}} {\frac {7}{1}}\times {\frac {4}{3}}={\frac {28}{3}}
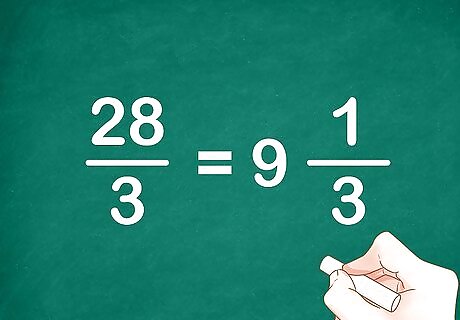
Simplify, if necessary. If you have an improper fraction (a fraction with a larger numerator than denominator), your teacher may require you to change it to a mixed number. Usually your teacher will require you to reduce proper fractions to lowest terms. For example, 28 3 {\displaystyle {\frac {28}{3}}} {\frac {28}{3}} simplifies to the mixed number 9 1 3 {\displaystyle 9{\frac {1}{3}}} 9{\frac {1}{3}}. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Simplifying a fraction just changes the way the fraction is written. To simplify a fraction, you can cancel out the greatest common factor from the numerator and denominator or convert an improper fraction to a mixed number. This doesn't change the inherent value of the fraction.
Drawing a Diagram
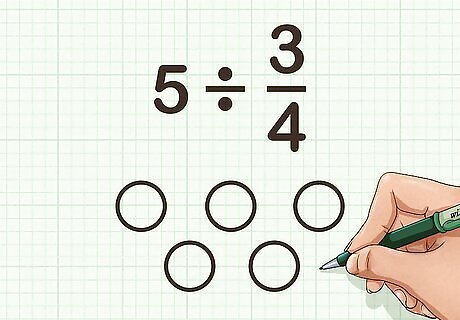
Draw shapes representing the whole number. Your shape should be one capable of dividing into equal groups, such as a square or circle. Draw the shapes large enough that you can divide them into smaller pieces. For example, if you are calculating 5 ÷ 3 4 {\displaystyle 5\div {\frac {3}{4}}} 5\div {\frac {3}{4}}, you would draw 5 circles.
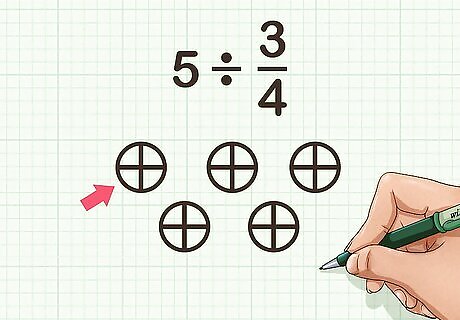
Divide each whole shape according to the fraction’s denominator. The denominator of a fraction tells you how many pieces a whole is divided into. Divide each whole shape into its fractional parts. For example, if you are dividing by 3 4 {\displaystyle {\frac {3}{4}}} {\frac {3}{4}}, the 4 in the denominator tells you to divide each whole shape into fourths.
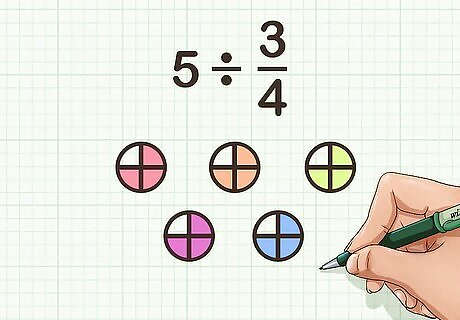
Shade in groups representing the fraction. Since you are dividing the whole number by the fraction, you are looking to see how many groups of the fraction are in the whole number. So, first, you need to create your groups. It might be helpful to shade each group a different color, since some groups will have pieces in two different wholes. Leave any leftover pieces unshaded. For example, if you are dividing 5 by 3 4 {\displaystyle {\frac {3}{4}}} {\frac {3}{4}}, you would color 3 quarters a different color for each group. Note that many groups will contain 2 quarters in one whole, and 1 quarter in another whole.
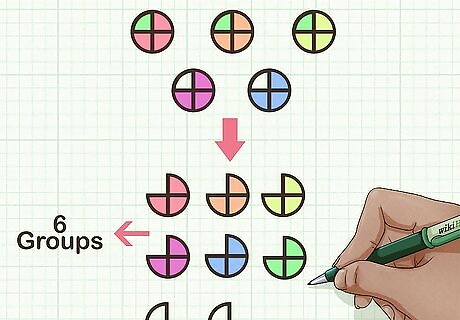
Count the number of whole groups. This will give you the whole number of your answer. For example, you should have created 6 groups of 3 4 {\displaystyle {\frac {3}{4}}} {\frac {3}{4}} among your 5 circles.
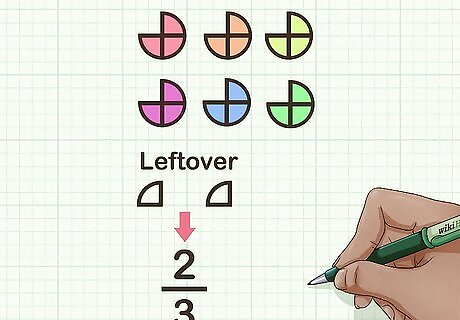
Interpret leftover pieces. Compare the number of pieces you have left over to a complete group. The fraction of a group that you have left over will indicate the fraction of your answer. Make sure you do not compare the number of pieces you have to a whole shape, as this will give you the wrong fraction. For example, after dividing the 5 shapes into groups of 3 4 {\displaystyle {\frac {3}{4}}} {\frac {3}{4}}, you have 2 quarters, or 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}} left. Since a whole group is 3 pieces, and you have 2 pieces, your fraction is 2 3 {\displaystyle {\frac {2}{3}}} {\frac {2}{3}}.
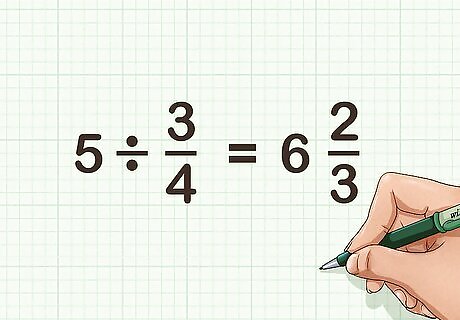
Write the answer. Combine your whole number of groups with your fractional number of groups to find the quotient of your original division problem. For example, 5 ÷ 3 4 = 6 2 3 {\displaystyle 5\div {\frac {3}{4}}=6{\frac {2}{3}}} 5\div {\frac {3}{4}}=6{\frac {2}{3}}.
Solving Sample Problems
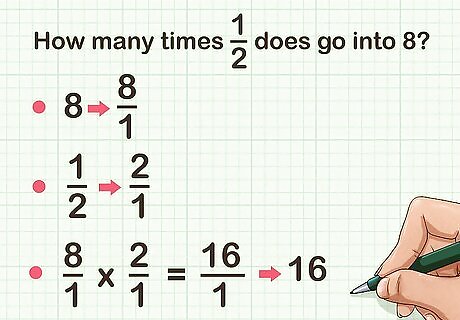
Solve this math problem: How many times does 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}} go into 8 {\displaystyle 8} 8? Since the problem is asking how many groups of 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}} are in 8, the problem is one of division. Turn 8 into a fraction by placing it over 1: 8 = 8 1 {\displaystyle 8={\frac {8}{1}}} 8={\frac {8}{1}}. Find the reciprocal of the fraction by reversing the numerator and denominator: 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}} becomes 2 1 {\displaystyle {\frac {2}{1}}} {\frac {2}{1}}. Multiply the two fractions together: 8 1 × 2 1 = 16 1 {\displaystyle {\frac {8}{1}}\times {\frac {2}{1}}={\frac {16}{1}}} {\frac {8}{1}}\times {\frac {2}{1}}={\frac {16}{1}}. Simplify, if necessary: 16 1 = 16 {\displaystyle {\frac {16}{1}}=16} {\frac {16}{1}}=16.
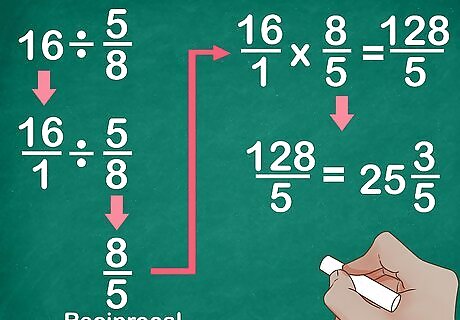
Solve the following problem: 16 ÷ 5 8 {\displaystyle 16\div {\frac {5}{8}}} 16\div {\frac {5}{8}}. Convert 16 into a fraction by placing it over 1: 16 = 16 1 {\displaystyle 16={\frac {16}{1}}} 16={\frac {16}{1}}. Take the fraction’s reciprocal by reversing the numerator and denominator: 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}} becomes 8 5 {\displaystyle {\frac {8}{5}}} {\frac {8}{5}}. Multiply the two fractions together: 16 1 × 8 5 = 128 5 {\displaystyle {\frac {16}{1}}\times {\frac {8}{5}}={\frac {128}{5}}} {\frac {16}{1}}\times {\frac {8}{5}}={\frac {128}{5}}. Simplify, if necessary: 128 5 = 25 3 5 {\displaystyle {\frac {128}{5}}=25{\frac {3}{5}}} {\frac {128}{5}}=25{\frac {3}{5}}.

Solve the following problem by drawing a diagram. Rufus has 9 cans of food. She eats 2 3 {\displaystyle {\frac {2}{3}}} {\frac {2}{3}} of a can every day. How many days will her food last? Draw 9 circles representing the 9 cans. Since she eats 2 3 {\displaystyle {\frac {2}{3}}} {\frac {2}{3}} at a time, divide each circle into thirds. Color groups of 2 3 {\displaystyle {\frac {2}{3}}} {\frac {2}{3}}. Count the number of complete groups. There should be 13. Interpret the leftover pieces. There is 1 piece leftover, which is 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}. Since a whole group is 2 3 {\displaystyle {\frac {2}{3}}} {\frac {2}{3}}, you have half a group left over. So, your fraction is 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}. Combine the number of whole groups and fractional groups to find your final answer: 9 ÷ 2 3 = 13 1 2 {\displaystyle 9\div {\frac {2}{3}}=13{\frac {1}{2}}} 9\div {\frac {2}{3}}=13{\frac {1}{2}}.



















Comments
0 comment