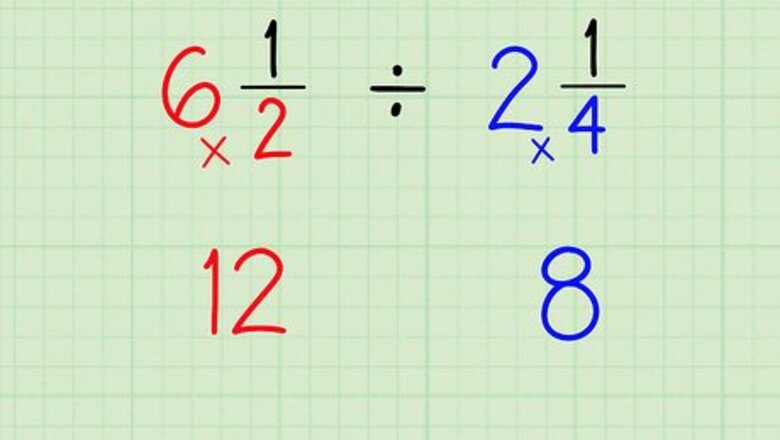
views
Converting Mixed Numbers to Improper Fractions

Multiply the whole number by the denominator of its combined fraction. Do this for both mixed numbers. Set these products aside. They are only part of your new numerator. For example, if you want to calculate 6 1 2 ÷ 2 1 4 {\displaystyle 6{\frac {1}{2}}\div 2{\frac {1}{4}}} 6{\frac {1}{2}}\div 2{\frac {1}{4}}, you would multiply 6 × 2 = 12 {\displaystyle 6\times 2=12} 6\times 2=12 and 2 × 4 = 8 {\displaystyle 2\times 4=8} 2\times 4=8.
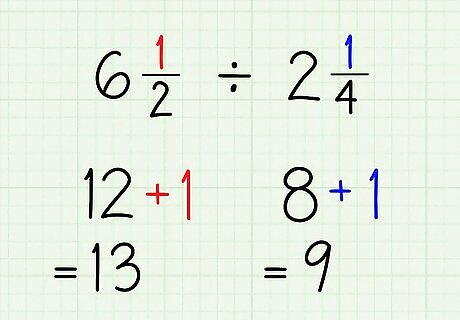
Add the numerator to the product.Do this for both mixed numbers. This sum will be the numerator of your improper fraction. For example, 12 + 1 = 13 {\displaystyle 12+1=13} 12+1=13 and 8 + 1 = 9 {\displaystyle 8+1=9} 8+1=9.
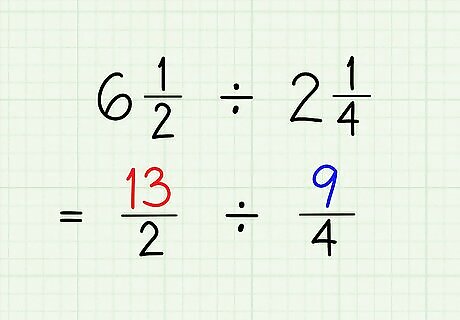
Place the sum over the original denominator. Complete this step for both fractions, making sure you use the correct denominators. These are your improper fractions that you will use to complete the division. For example, 6 1 2 {\displaystyle 6{\frac {1}{2}}} 6{\frac {1}{2}} becomes 13 2 {\displaystyle {\frac {13}{2}}} {\frac {13}{2}} and 2 1 4 {\displaystyle 2{\frac {1}{4}}} 2{\frac {1}{4}} becomes 9 4 {\displaystyle {\frac {9}{4}}} {\frac {9}{4}}.
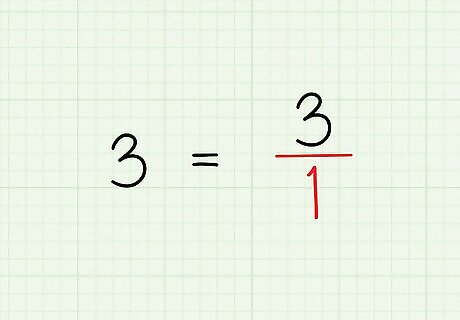
Convert whole numbers to fractions. If you are working with any whole numbers, you need to convert them to fractions. To do this, turn the number into the numerator of a fraction. The denominator will be 1. For example, 3 = 3 1 {\displaystyle 3={\frac {3}{1}}} 3={\frac {3}{1}}.
Dividing Improper Fractions
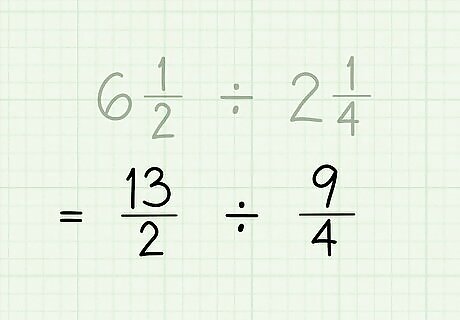
Write the new division problem. Use the improper fractions you found by completing the calculations in Part 1. For example, 13 2 ÷ 9 4 {\displaystyle {\frac {13}{2}}\div {\frac {9}{4}}} {\frac {13}{2}}\div {\frac {9}{4}}.
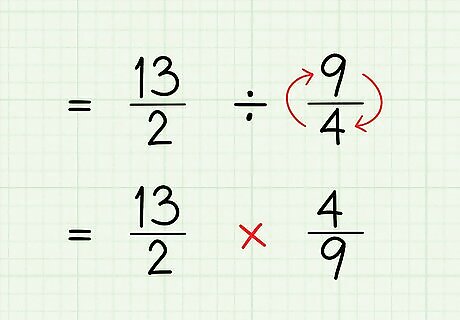
Take the reciprocal of the second fraction. To find a reciprocal of a fraction, you need to “flip” it, so that the numerator becomes the denominator, and the denominator becomes the numerator. Then, change the problem to a multiplication problem. For example, if you take the reciprocal of 9 4 {\displaystyle {\frac {9}{4}}} {\frac {9}{4}}, it becomes 4 9 {\displaystyle {\frac {4}{9}}} {\frac {4}{9}}. So 13 2 ÷ 9 4 {\displaystyle {\frac {13}{2}}\div {\frac {9}{4}}} {\frac {13}{2}}\div {\frac {9}{4}} becomes 13 2 × 4 9 {\displaystyle {\frac {13}{2}}\times {\frac {4}{9}}} {\frac {13}{2}}\times {\frac {4}{9}}
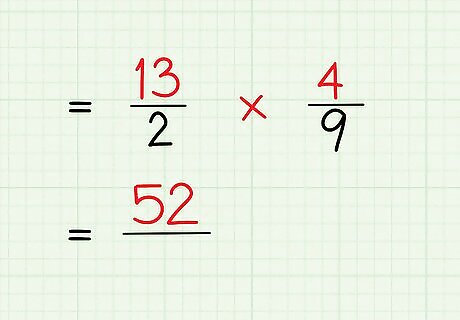
Multiply the numerators. To do this, multiply them as if they were whole numbers. This product will be the numerator of your answer. For example, if calculating 13 2 × 4 9 {\displaystyle {\frac {13}{2}}\times {\frac {4}{9}}} {\frac {13}{2}}\times {\frac {4}{9}}, you would multiply the numerators: 13 × 4 = 52 {\displaystyle 13\times 4=52} 13\times 4=52.
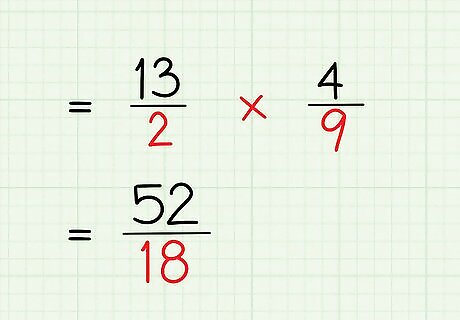
Multiply the denominators. To do this, multiply them as if they were whole numbers. This product will be the denominator of your answer. For example, if calculating 13 2 × 4 9 {\displaystyle {\frac {13}{2}}\times {\frac {4}{9}}} {\frac {13}{2}}\times {\frac {4}{9}}, you would multiply the denominators: 2 × 9 = 18 {\displaystyle 2\times 9=18} 2\times 9=18. Putting together your numerator and denominator, your answer becomes 52 18 {\displaystyle {\frac {52}{18}}} {\frac {52}{18}}.
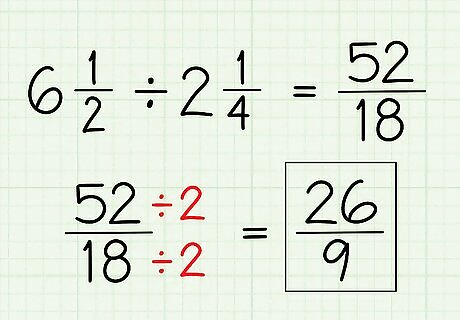
Simplify your answer, if possible. To simplify, or reduce, a fraction, you need to find the greatest factor (besides 1) that is common to the numerator and the denominator. Then, divide the numerator and denominator by that factor. For more information on this process, read Reduce Fractions. For example, 52 {\displaystyle 52} 52 and 18 {\displaystyle 18} 18 are both divisible by 2 {\displaystyle 2} 2. 52 ÷ 2 = 26 {\displaystyle 52\div 2=26} 52\div 2=26 18 ÷ 2 = 9 {\displaystyle 18\div 2=9} 18\div 2=9So, 52 18 = 26 9 {\displaystyle {\frac {52}{18}}={\frac {26}{9}}} {\frac {52}{18}}={\frac {26}{9}} EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Simplifying a fraction just changes the way the fraction is written. To simplify a fraction, you can cancel out the greatest common factor from the numerator and denominator or convert an improper fraction to a mixed number. This doesn't change the inherent value of the fraction.
Converting Improper Fractions Back Into Mixed Numbers
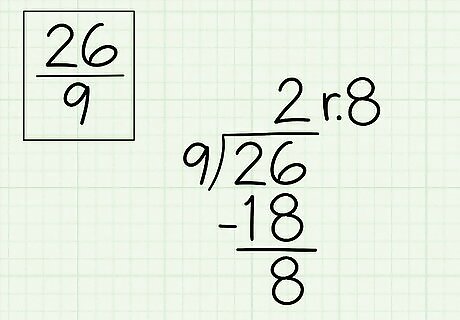
Divide the numerator by the denominator. If there is no remainder, then your answer is a whole number rather than a mixed number, and you need not do anything further. Likely, though, you will have a remainder. Set this aside for now. The quotient you found when Dividing the numerator by the denominator will be the whole number of your mixed number. For example, 26 ÷ 9 = 2 {\displaystyle 26\div 9=2} 26\div 9=2 with a remainder of 8 {\displaystyle 8} 8. Thus, the whole number of your mixed number will be 2.
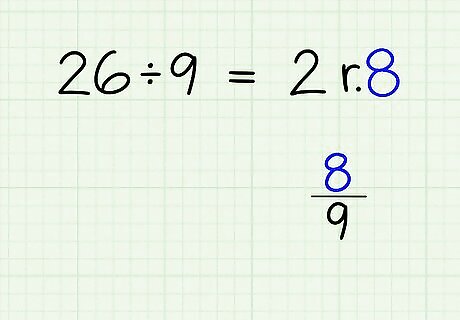
Turn the remainder into the numerator of your fraction. Place this numerator over the original denominator. This will give you the fraction of your mixed number. For example, if your original denominator is 9 {\displaystyle 9} 9 and your remainder is 8 {\displaystyle 8} 8, the fraction of your mixed number is 8 9 {\displaystyle {\frac {8}{9}}} {\frac {8}{9}}.
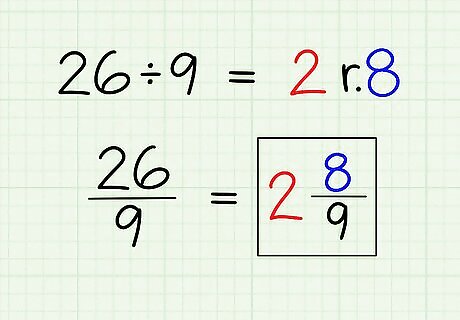
Combine the whole number and the fraction. This gives you the final answer to your original division problem.

















Comments
0 comment