
views
Pythagorean Theorem
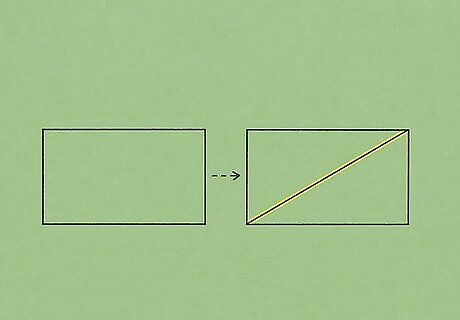
Mark the diagonal on the rectangle. If you have a visual of your rectangle, it will be a lot easier to figure out the area given a diagonal. Draw out a rectangle (it doesn’t have to match the proportions given, just a rectangle shape will do) and mark out a diagonal line to create 2 triangles. You’ll be able to see the 2 triangles that make up the rectangle now.
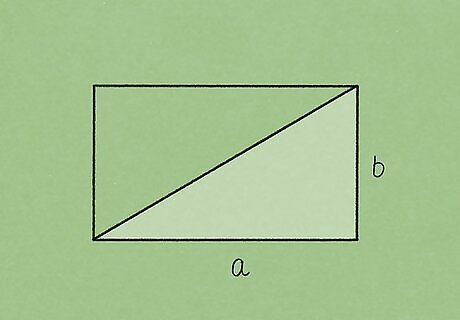
Assign 2 sides of the triangle as a {\displaystyle a} {\displaystyle a} and b {\displaystyle b} {\displaystyle b}. Pick one of the triangles that you’ve created in your rectangle to work with. Assign one side as a {\displaystyle a} {\displaystyle a} and the other side as b {\displaystyle b} {\displaystyle b}. Make sure that you know either the length or width value as well as the diagonal value to solve your equation. If you were working with a square, you could assign both sides of the triangle as a {\displaystyle a} {\displaystyle a} since they are both the same. You can use the Pythagorean Theorem because you’re working with a right angle triangle.

Plug the 2 measurements into the Pythagorean Theorem. The Pythagorean Theorem states that a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} {\displaystyle a^{2}+b^{2}=c^{2}}. In this instance, the height and width of the triangle are a {\displaystyle a} {\displaystyle a} and b {\displaystyle b} {\displaystyle b}, while c {\displaystyle c} {\displaystyle c} is the diagonal. Let’s say the diagonal is 10 inches and the length is 8 inches. The equation would look like this: a 2 + 8 2 = 10 2 {\displaystyle a^{2}+8^{2}=10^{2}} {\displaystyle a^{2}+8^{2}=10^{2}}.
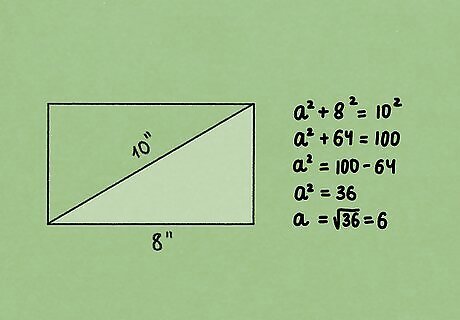
Solve the equation to find the missing side. Break down every number to its simplest form one step at a time to solve for the missing expression. When you’re done, you can assign the answer to the missing side on your rectangle. For example: a 2 + 8 2 = 10 2 {\displaystyle a^{2}+8^{2}=10^{2}} {\displaystyle a^{2}+8^{2}=10^{2}}. a 2 + 64 = 100 {\displaystyle a^{2}+64=100} {\displaystyle a^{2}+64=100}. a 2 = 100 − 64 {\displaystyle a^{2}=100-64} {\displaystyle a^{2}=100-64}. a 2 = 36 {\displaystyle a^{2}=36} {\displaystyle a^{2}=36}. a 2 = 36 {\displaystyle {\sqrt {a^{2}}}={\sqrt {36}}} {\displaystyle {\sqrt {a^{2}}}={\sqrt {36}}}. a = 6 {\displaystyle a=6} {\displaystyle a=6}.
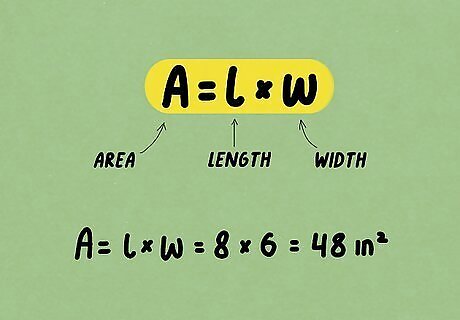
Plug the new number into A = l × w {\displaystyle A=l\times w} A=l\times w. To find the area of your entire rectangle, you need to solve for Area = length x width, or A = l x w. Now that you’ve used the Pythagorean Theorem to find the second side length, you can solve for the area. Don’t forget your units! For example: A = 8 × 6 {\displaystyle A=8\times 6} {\displaystyle A=8\times 6}. A = 48 i n 2 {\displaystyle A=48\ in^{2}} {\displaystyle A=48\ in^{2}}. Area is always in units squared. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Use this visual trick to understand the Pythagorean Theorem. Imagine a right triangle with squares constructed on each leg and the hypotenuse. by rearranging the smaller squares within the larger square, the areas of the smaller squares (a² and b²) will add up visually to the area of the larger square (c²).
Alternative Area Formula
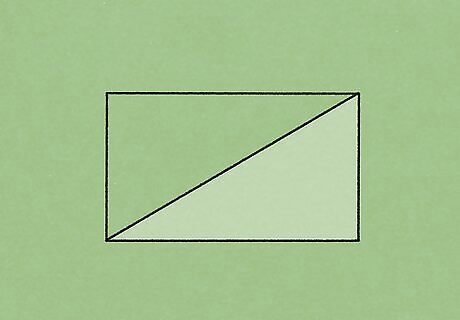
Mark the diagonal and side length on your rectangle. If you have a visual in front of you, it will be much easier to see how you’re solving your equation. Draw a simple rectangle with a ruler and create a diagonal line across it to make 2 triangles. It’s not mandatory to draw your triangle, but it can help you, especially if you’re just starting out.

Enter the length and diagonal into A = l × d 2 − l 2 {\displaystyle A=l\times {\sqrt {d^{2}-l^{2}}}} {\displaystyle A=l\times {\sqrt {d^{2}-l^{2}}}}. Simply plug the length and the diagonal into the formula above. Remember, the diagonal is always longer than the length of the rectangle. For example, if the length is 8 inches and the diagonal is 10 inches, the formula would be A = 8 × 10 2 − 8 2 {\displaystyle A=8\times {\sqrt {10^{2}-8^{2}}}} {\displaystyle A=8\times {\sqrt {10^{2}-8^{2}}}}.
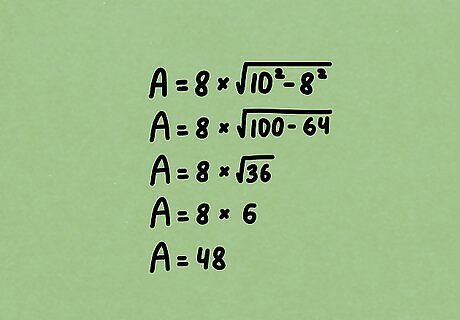
Solve the equation to find the area. All you have to do now is break down the equation (using PEMDAS) in order to simplify it and get the area of the rectangle. For example: A = 8 × 10 2 − 8 2 {\displaystyle A=8\times {\sqrt {10^{2}-8^{2}}}} {\displaystyle A=8\times {\sqrt {10^{2}-8^{2}}}}. A = 8 × 36 {\displaystyle A=8\times {\sqrt {36}}} {\displaystyle A=8\times {\sqrt {36}}}. A = 8 × 6 {\displaystyle A=8\times 6} {\displaystyle A=8\times 6}. A = 48 {\displaystyle A=48} {\displaystyle A=48}.



















Comments
0 comment