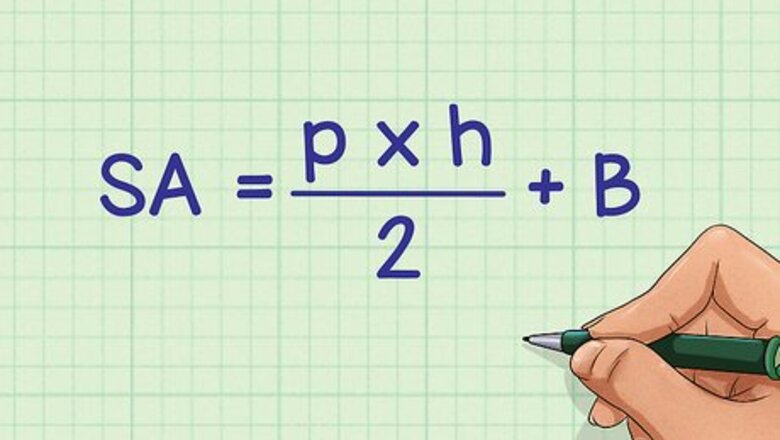
views
Finding the Surface Area of Any Regular Pyramid
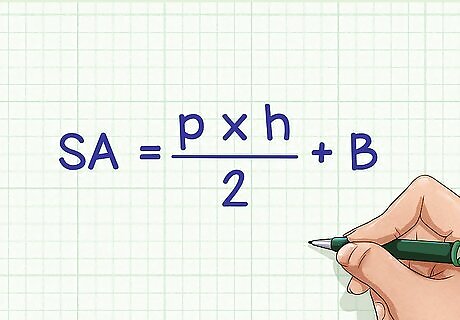
Set up the formula for the surface area of a regular pyramid. The formula is S A = p × h 2 + B {\displaystyle SA={\frac {p\times h}{2}}+B} SA={\frac {p\times h}{2}}+B, where S A {\displaystyle SA} SA equals the total surface area of the pyramid, p {\displaystyle p} p equals the perimeter of the base, h {\displaystyle h} h equals the slant height of the pyramid, and B {\displaystyle B} B equals the area of the base. The basic formula for the surface area of any pyramid, regular or irregular, is Total Surface Area = Base Area + Lateral Area. Don’t confuse “slant height” with “height.” The “slant height” of a regular pyramid is the shortest possible distance from the apex of the pyramid to the edge of the base. The “height” of a regular pyramid is the distance from the vertex to the center of the base.
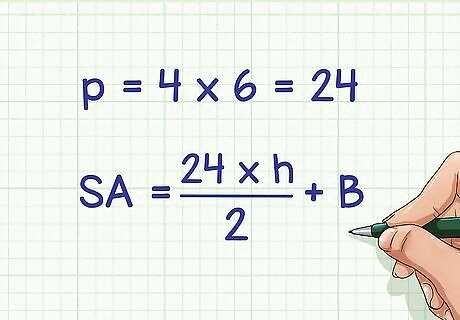
Plug the perimeter of the base into the formula. If you aren’t given the perimeter but know the length of one edge of the base, you can calculate the perimeter by multiplying the length of one edge by the number of edges. For example, If you are finding the surface area of a hexagonal pyramid, and you know that the length of one edge of the base is 4 cm, you would calculate 4 × 6 = 24 {\displaystyle 4\times 6=24} 4\times 6=24 to find the perimeter of the base, since a hexagon has six edges, or sides. Thus, the perimeter of the base is 24 cm, so your surface area formula will look like this: S A = 24 × h 2 + B {\displaystyle SA={\frac {24\times h}{2}}+B} SA={\frac {24\times h}{2}}+B.
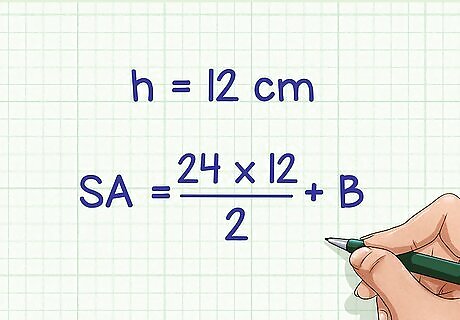
Plug the value of the slant height into the formula. Make sure you are using the slant height, not the perpendicular height. The problem should provide the slant height. If you don’t know the slant height, you cannot use this method. For example, if the slant height of a hexagonal pyramid is 12 cm, your formula will look like this: S A = 24 × 12 2 + B {\displaystyle SA={\frac {24\times 12}{2}}+B} SA={\frac {24\times 12}{2}}+B.

Calculate the area of the base. How you do this will depend on the shape of the base. To learn more about finding the area of a polygon, read Find the Area of Regular Polygons. For example, if you are working with a hexagonal pyramid, the base is a hexagon. To find out how to calculate the area of the base, you can read Calculate the Area of a Hexagon. The formula is A = 3 3 × s 2 2 {\displaystyle A={\frac {3{\sqrt {3}}\times s^{2}}{2}}} A={\frac {3{\sqrt {3}}\times s^{{2}}}{2}}, where s {\displaystyle s} s is the length of one side of the hexagon. Since the length of one side of the hexagon is 4 cm, you would calculate: A = 3 3 × 4 2 2 {\displaystyle A={\frac {3{\sqrt {3}}\times 4^{2}}{2}}} A={\frac {3{\sqrt {3}}\times 4^{{2}}}{2}} A = 3 3 × 16 2 {\displaystyle A={\frac {3{\sqrt {3}}\times 16}{2}}} A={\frac {3{\sqrt {3}}\times 16}{2}} A = 48 3 2 {\displaystyle A={\frac {48{\sqrt {3}}}{2}}} A={\frac {48{\sqrt {3}}}{2}} A = 83.14 2 {\displaystyle A={\frac {83.14}{2}}} A={\frac {83.14}{2}} A = 41.57 {\displaystyle A=41.57} A=41.57.So the area of the base is 41.57 square centimeters. EXPERT TIP Grace Imson, MA Grace Imson, MA Math Instructor, City College of San Francisco Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. Grace Imson, MA Grace Imson, MA Math Instructor, City College of San Francisco Our Expert Agrees: The surface area of a pyramid is equal to the sum of the areas of all of the faces. First, you have to get the area of the base, then add the area of the lateral sides, which is one face times the number of sides.

Plug the area of the base into the formula. Make sure you substitute for the variable B {\displaystyle B} B. For example, if the area of the hexagonal base is 41.57 sq. cm., your formula for surface area will now look like this: S A = 24 × 12 2 + 41.57 {\displaystyle SA={\frac {24\times 12}{2}}+41.57} SA={\frac {24\times 12}{2}}+41.57.

Multiply the perimeter of the base and the slant height of the pyramid. Then, divide by two. This will give you the lateral surface area of the pyramid. For example: S A = 24 × 12 2 + 41.57 {\displaystyle SA={\frac {24\times 12}{2}}+41.57} SA={\frac {24\times 12}{2}}+41.57 S A = 288 2 + 41.57 {\displaystyle SA={\frac {288}{2}}+41.57} SA={\frac {288}{2}}+41.57 S A = 144 + 41.57 {\displaystyle SA=144+41.57} SA=144+41.57

Add the two values together. The sum will be the lateral surface area, plus the base surface area, providing you with the total surface area for the pyramid, in square units. For example: S A = 144 + 41.57 {\displaystyle SA=144+41.57} SA=144+41.57 S A = 185.57 {\displaystyle SA=185.57} SA=185.57So, the total surface area of a hexagonal pyramid, given a base edge length of 4 cm and a slant height of 12 cm, is 185.57 square centimeters.
Finding the Surface Area of a Square Pyramid
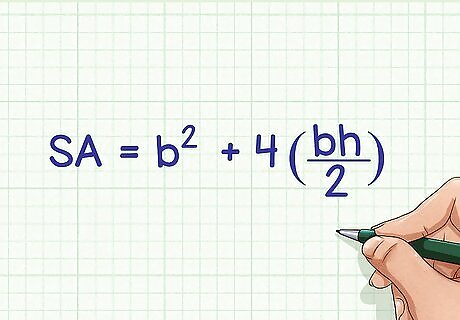
Set up the formula for surface area of a square pyramid. The formula is S A = b 2 + 4 ( b h 2 ) {\displaystyle SA=b^{2}+4({\frac {bh}{2}})} SA=b^{{2}}+4({\frac {bh}{2}}), where b {\displaystyle b} b is equal to the length of one side of the base, and h {\displaystyle h} h is equal to the slant height of the pyramid. Don’t confuse “slant height” with “height.” The “slant height” is the diagonal distance from the apex of the pyramid to the edge of the base. The “height” is the perpendicular distance from the vertex to the base. Note that this formula is just another way of writing Total Surface Area = Base Area ( b 2 {\displaystyle b^{2}} b^{{2}}) + Lateral Area ( 4 ( b h 2 ) {\displaystyle 4({\frac {bh}{2}})} 4({\frac {bh}{2}})). This formula only works for regular square pyramids.
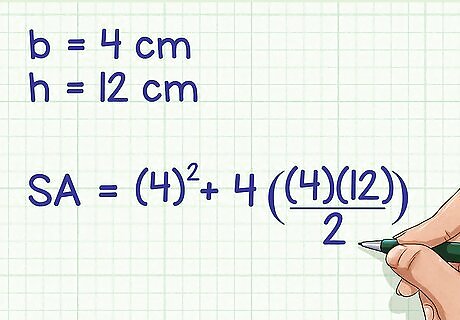
Plug in the values for the side length and slant height into the formula. Make sure you substitute the side length of the base for b {\displaystyle b} b and the slant height for h {\displaystyle h} h. For example, if the length of one side of the base of a square pyramid is 4 cm, and the slant height is 12 cm, the formula will look like this: S A = 4 2 + 4 ( ( 4 ) ( 12 ) 2 ) {\displaystyle SA=4^{2}+4({\frac {(4)(12)}{2}})} SA=4^{{2}}+4({\frac {(4)(12)}{2}}).
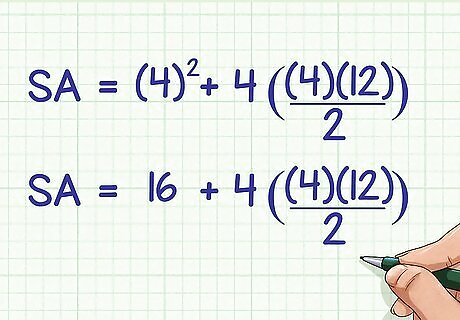
Square the side length of the base. This will give you the surface area of the base. For example: S A = 4 2 + 4 ( ( 4 ) ( 12 ) 2 ) {\displaystyle SA=4^{2}+4({\frac {(4)(12)}{2}})} SA=4^{{2}}+4({\frac {(4)(12)}{2}}) S A = 16 + 4 ( ( 4 ) ( 12 ) 2 ) {\displaystyle SA=16+4({\frac {(4)(12)}{2}})} SA=16+4({\frac {(4)(12)}{2}})

Multiply the side length of the base by the slant height and divide by two. Then, multiply by 4. This will give you the lateral surface area of the pyramid. For example: S A = 16 + 4 ( ( 4 ) ( 12 ) 2 ) {\displaystyle SA=16+4({\frac {(4)(12)}{2}})} SA=16+4({\frac {(4)(12)}{2}}) S A = 16 + 4 ( 48 2 ) {\displaystyle SA=16+4({\frac {48}{2}})} SA=16+4({\frac {48}{2}}) S A = 16 + 4 ( 24 ) {\displaystyle SA=16+4(24)} SA=16+4(24) S A = 16 + 96 {\displaystyle SA=16+96} SA=16+96

Add the base surface area and the lateral surface area. This will give you the total surface area of the pyramid, in square units. For example: S A = 16 + 96 {\displaystyle SA=16+96} SA=16+96 S A = 112 {\displaystyle SA=112} SA=112So, the total surface area of a square pyramid, with a base side length of 4 cm and a slant height of 12 cm, is 112 square centimeters.

















Comments
0 comment