How to Annualize a Quarterly Return

Editor

posted on 12 years ago — updated on 1 second ago

14
views

Investment companies provide their clients with regular updates regarding their return on investment (ROI). If you have investments, you probably have received a quarterly return report that shows how well each of your investments has fared over the preceding three months. It is easier to comprehend the strength of the investment (as well as to compare it with other investments) if you can translate the quarterly return into an equivalent annual return. You can do this with a calculator or even pencil and paper.

Things You Should Know

Annualizing a quarterly return will give you a sense for how an investment will perform over the course of the year if all things stay the same.
The formula for an annual rate of return is: Annual Rate of Return = [(1 + Quarterly Rate of Return)^4] – 1.
You can replace the quarterly rate of return with a daily rate of return to get a sense for the annual return of an investment after a few days.
Remember, investments can change in value over time and an annualized return is not an automatic given.^{[1]
X
Research source}

Locating the Information

Obtain the investment's quarterly report. You will receive this in the mail or you can look it up online under your account. You can also find this information on the company's website.

Find the quarterly rate of return. There will likely be a number of figures within the report that show how the investment rose or fell during that time. What you want to annualize is the percentage figure, called the rate of return (ROR), which shows the percentage of growth (or shrinkage) you received during the previous three months. For example, at the bottom of the page of numbers it may show that your quarterly return is 1.5 percent. The annual return would be larger, because your money could be expected to have grown each quarter. The annualized return would be the percentage of growth if the investment grew at the same rate all year.

Calculate how many time periods there are in a year. In order to annualize, you first consider the time period being featured. In this case it's three months since it's a quarterly report. Then calculate how many such periods are contained in a year. Thus, there are four three-month periods (quarters) in a year. You would then use the number 4 when called for in the annualizing formula. If you were trying to annualize a monthly return, you would use the number 12.

Calculating the Annual Rate of Return

Calculate the annual rate of return. For a quarterly investment, the formula to calculate the annual rate of return is: Annual Rate of Return = [(1 + Quarterly Rate of Return)^4] - 1. The number 4 is an exponent. In other words, the quantity "1 + quarterly rate of return" is raised to the fourth power, and then 1 is subtracted from the result.

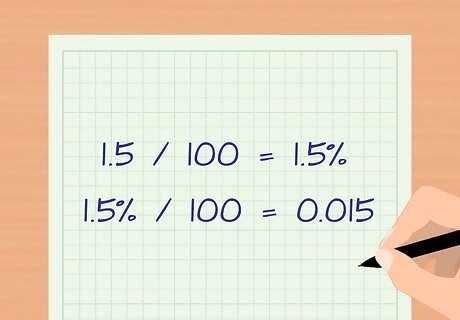
Turn your quarterly ROR into a decimal. Again let's say your quarterly ROR is 1.5%. First divide 1.5 by divide it by 100. 1.5 percent divided by 100 is 0.015.

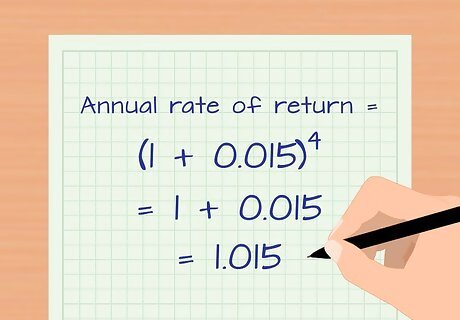
Plug in your numbers. Continuing this example, use 0.015 as the quarterly ROR. Thus, the annual rate of return = (1 + 0.015) raised to the fourth power. Add 1 to 0.015 and you get 1.015.

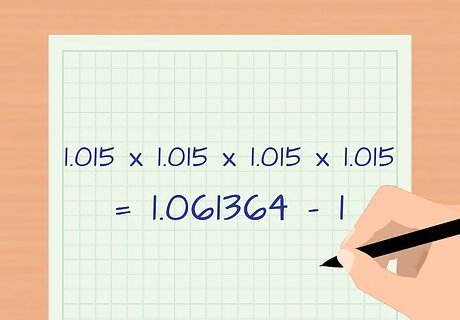
Use a calculator to bring that number to the fourth power. If you do not have a calculator that works with exponents, you can search for one on the Internet or buy one at your local office supplies store. 1.015 to the fourth power is 1.061364. You can always multiply 1.015 x 1.015 x 1.015 x 1.015 if you don't have a calculator. The example formula now looks like this: Annual Rate Of Return = 1.061364 - 1.

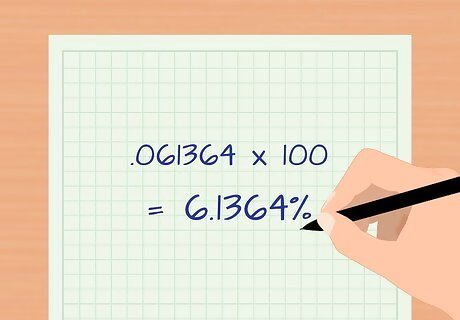
Subtract 1 from your result. This equals .061364. This is your annual ROR expressed as a decimal. Multiply that decimal by 100 to get your percent rate of return. In our example, .061364 x 100 = 6.1364% for the annual rate of return.

Annualizing Daily Returns

Calculate the Annual Rate of Return using days. You may have a new investment and want to know the Annual Rate of Return based on a number of days, not months. Let's say you have held the investment for 17 days and earned 2.13%.

Plug the numbers into the formula. In this case to calculate the exponent to use, you will divide 17 (the number of days you held the investment) by 365 (the number of days in a year). The answer is .0465753. Convert 2.13% interest rate to a decimal by dividing 2.13 by 100 = .0213. Your formula will look like this: ((1+0.0213)^1/.0465753) – 1 = Annual Rate of Return. ((1.0213)^21.4706078)-1 = 1.5722717 - 1 = .5722717. Convert this to a percentage by multiplying this by 100 = 57.23% annual rate of return.

Use caution when annualizing returns. You can't assume that just because you earned 2.13% in a number of days or months that you will be able to earn that same amount the rest of the year. Stock earnings go up and down every day but you will be able to make a general projection.

Original news source