How to Calculate the Area of a Scalene Triangle

Rustopte

Editor

posted on 10 years ago — updated on 1 second ago

40
views

A triangle with no equal sides and angles is called a scalene triangle. There are three ways that you can figure out the area of this kind of triangle, but the method you use depends on what values you are given in the problem you are trying to solve. Some problems will give you the length of one side (the base) and the height of the triangle. Another kind of problem will give you the length of two sides and one angle. The last kind of problem will give you the length of all three sides. Scroll down to Step 1 to learn how to solve all of these problems.

Steps

When Length of One Side and Height are Given

Understand the equation you will use to solve this equation. You will use the equation K=bh/2. K is the area of the triangle while b is the base and h is the height of the triangle. Let’s look at an example: Let’s say you were given a problem where you have to find the area of a triangle (K) that has one side that is 6 inches (15.2 cm), and a height of 5 inches (12.7 cm). That means that b = 6 and h = 5.

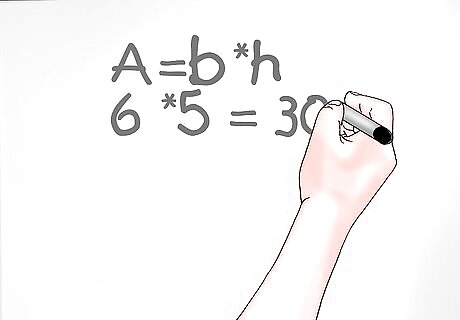
Multiply the base times the height. To find the area of this triangle, you must start by multiplying the base times the height. This will give you the area of a polygon (such as a rectangle). The area of a scalene triangle is half the area of a polygon. Let’s look at our example: Remember to do this, you will use the equation b * h. Therefore, our equation is 6 *5 = 30.

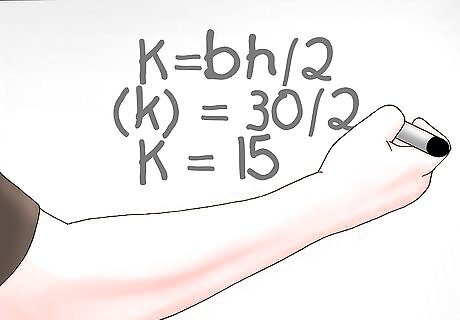
Divide the product of multiplying the base and height by two to solve the equation. As stated above, multiplying the base times the height will only give you the area of a rectangle with the same measurements as your triangle. To find the triangle’s area, you will have to divide the product of the base and height by two. As a reminder, your equation is K=bh/2. Let’s solve our example equation: K=bh/2 so our equation is the area of the triangle (k) = 30/2, therefore K = 15.

When Length of Two Sides and One Angle are Given

Understand the equation you will use to solve this equation. You will use K=ab*(sinC/2) to solve this equation. ‘K’ is the area of the triangle, while ‘a’ and ‘b’ are the two given sides. You will also be given one angle of the triangle, which is represented by ‘C’. An angle is the shape formed by two lines or rays originating from one point, which is called the vertex. Let’s look at an example: Let’s say that are you are given a problem where side a = 6, side b = 5 and angle C is 70° angle between side a and side b.

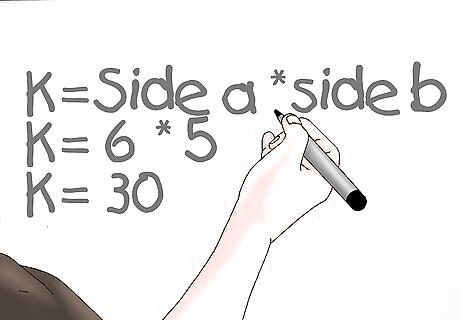
Multiply the two given sides. The first step towards finding the area of the triangle is to multiply the two known sides together. The equation for this is side a* side b. Our example is: Side a * side b = 6 * 5 = 30.

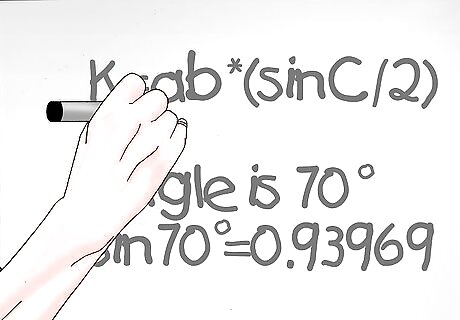
Determine the sine of the given angle. The sine of an angle is a trigonometric function that can be found by dividing the side of the triangle opposite the angle with the hypotenuse (or longest side) of the triangle. Luckily, you can figure out the sine of your angle with your calculator. If you have to find the sine by hand, click here. Let’s look at our example: The angle is 70° so our equation is sin70° = 0.93969.

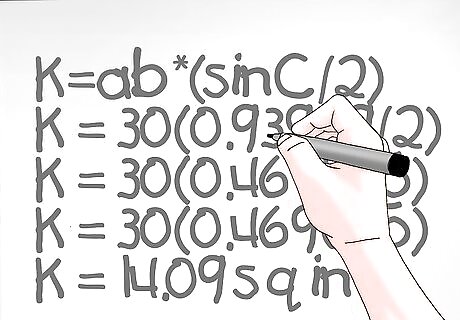
Multiply the product of the two sides with the sin of the angle, and then divide by 2 to solve the equation. We have now filled in all of the gaps of our equation. As a reminder, the equation is K=ab*(sinC/2). Let’s look at our example: K=ab*(sinC/2) so our full equation is K = 30(0.93969/2). First, let’s solve the equation inside the parentheses by dividing the sine of 70° by 2. (0.93969/2) = 0.469845. Now, we multiply that by 30 to find the area. K = 30(0.469845) so K = 14.09 inches (35.8 cm) squared.

When Length of Three Sides are Given

Understand the equation you will use to solve this problem. The equation for this type of math problem is K=S(s-a)(s-b)(s-c). K is the area and a, b, and c are the three sides of the triangle. Meanwhile, S will represent the semi-perimeter. You will need to find the semi-perimeter of the triangle to find the area (see Step 2). Let’s look at an example problem: Let’s say you are given a problem where the three sides of the triangle are a =3, b = 4, and c = 5.

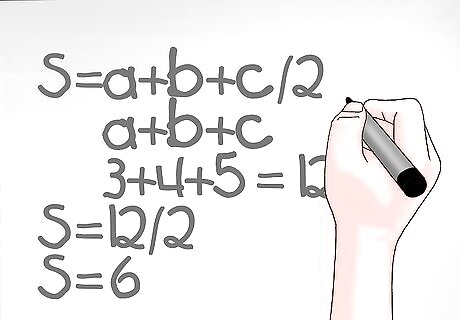
Calculate the semi-perimeter of the triangle. The equation for finding the semi-perimeter of the triangle is S=a+b+c/2. First, add up all three sides of the triangle. This means at a + b + c. Once you have added up all three numbers, divide the sum by 2. Let’s look at our example: Add up a+b+c: 3+4+5 = 12. Divide 12 by 2: 12/2 = 6. So the semi-perimeter (S) of the triangle is 6. S = 6.

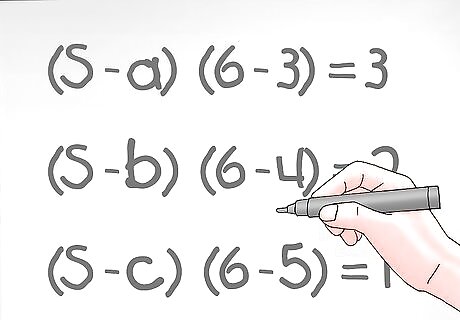
Find the difference of each side. You now have to find the difference for each side of the triangle based on the semi-perimeter that you just found. To do this, subtract the value of one side from the semi-perimeter. Write it down and do the same for the other two sides. To find side a: (S - a) is (6 - 3) = 3. To find side b: (S - b) is (6 - 4) = 2. To find side c: (S - c) is (6 - 5) = 1.

Multiply the semi-perimeter with the difference of each side. Once you have found the difference of each side, multiply the semi-perimeter to each of the numbers that you have found. This means that you multiply S to each individual number you have found. Let’s look at the example: S * (S-a)(S-b)(S-c) = 6(3)(2)(1) = 18+12+6 = 36.

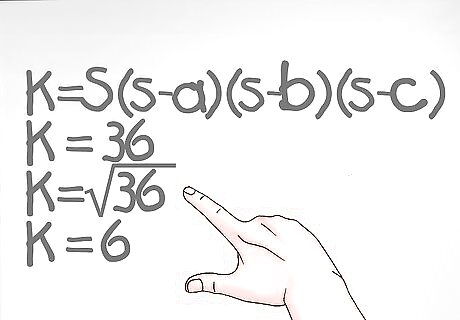
Take the square root of product of the semi-perimeter and the sides. Remember, the equation for the area is K=root[S(s-a)(s-b)(s-c)]. To find the square root, you can use a calculator unless your teacher wants you to do it by hand. If he or she wants you to do it by hand, click here to learn how. Let’s finish our example problem: We now have K = 36. The answer is therefore K = 6. The area of the triangle is 6.