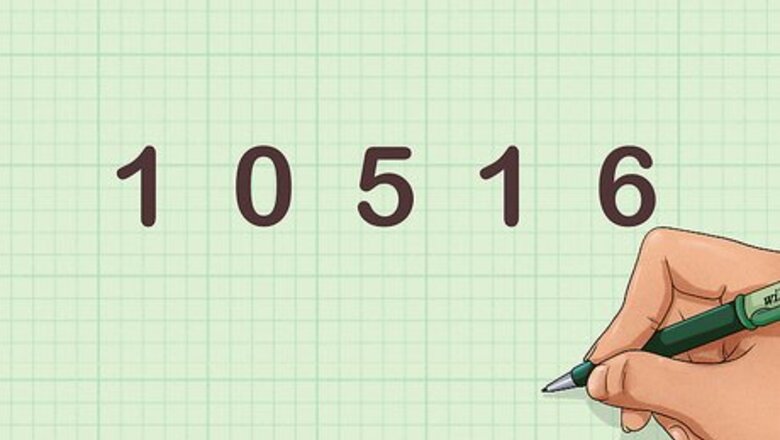
views
Using Alternating Sums
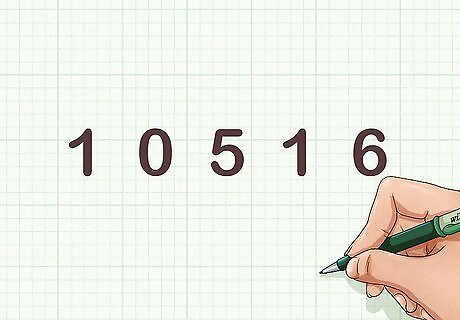
Write the number with spaces in between digits. For example, if you want to know whether 10,516 is divisible by 11, write the number like this:1 0 5 1 6
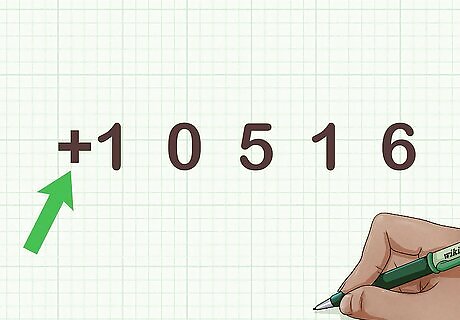
Write a + sign in front of the first digit. For example:+1 0 5 1 6

Write a - sign in front of the next digit. Your paper should now look like this:+1 - 0 5 1 6
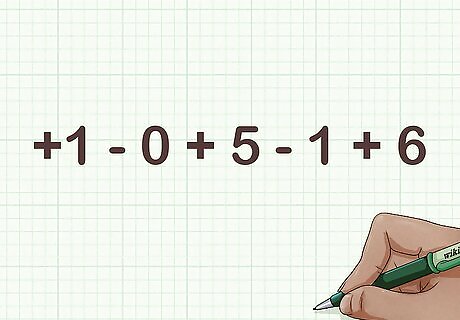
Keep alternating the + and - signs for all digits. Add a + sign in front of the third digit, then a - sign in front of the fourth, and so on until you reach the end:+1 - 0 + 5 - 1 + 6
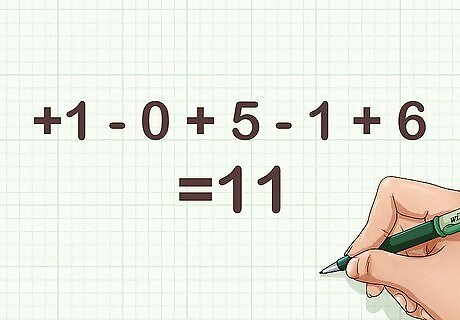
Add and subtract the digits. Now treat this like any arithmetic problem, adding and subtracting the digits together: +1 - 0 + 5 - 1 + 6= 11

Check your answer. These simple rules tell you whether the original number is divisible by 11: If your answer is divisible by 11 (0, 11, 22, etc.), the original number is also divisible by 11. Keep in mind that 0 is a multiple of 11, since 11 * 0 = 0. If your answer is not a multiple of 11, the original number is not divisible by 11. The answer was 11, which is a multiple of 11.Therefore, the original number 10,516 is divisible by 11.
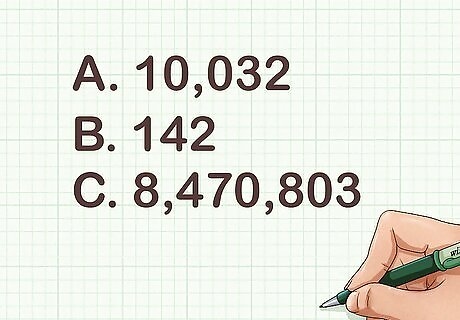
Solve example problems. Here are a couple practice problems. Try to solve them on your own, then check the answers below.Use the alternate sums method on each number to check whether it's divisible by 11:A. 10,032B. 142C. 8,470,803

Check your answers. Here are the answers to the practice problems: A. 10032+1 - 0 + 0 - 3 + 2 = 00 is divisible by 11, so yes, 10,032 is also divisible by 11.B. 142+1 - 4 + 2 = -1.-1 is not divisible by 11, so no, 142 is not divisible by 11.C. 8470803+8 - 4 + 7 - 0 + 8 - 0 + 3 = 2222 is divisible by 11, since 11 * 2 = 22. Yes, 8,470,803 is divisible by 11.
Using Pairs of Digits

Write down your number. For example, let's check whether 17952 is divisible by 11.
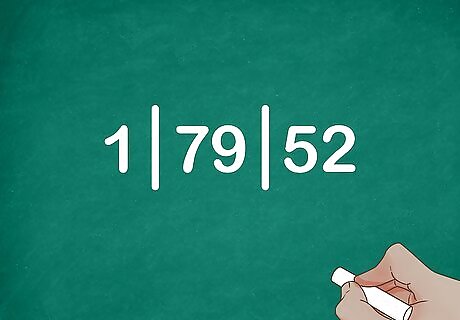
Divide the digits in pairs from right to left. Draw a vertical line to separate the two rightmost digits from the rest of the number. Move left two more spaces and draw another line. Repeat until the whole number is divided into pairs of digits. (The last digit on the left might be alone.) For 17952, start at the right (the ones place) and count two digits to the left, then draw a line: 179 | 52. Count left two more digits and draw another line: 1 | 79 | 52.
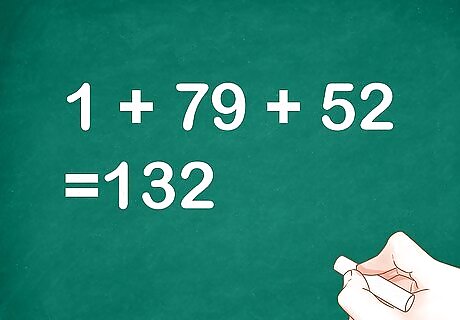
Add the numbers together. Treat each separate section as its own number. Add them together: 1 + 79 + 52 = 132.

Check whether the answer is divisible by 11. If it is, then the original number is divisible by 11 as well. If your answer is not divisible by 11, your original number is not either. If you're not sure whether the answer is divisible by 11, repeat these same steps to test it: Divide 132 into 1 | 32. Add these together to get 1 + 32 = 33. Since 33 is divisible by 11, then 132 is as well. Since 132 is divisible by 11, your original number 17952 is also divisible by 11.
















Comments
0 comment