views
X
Research source
Repeating decimals can be tricky to work with, but they can also be converted into a fraction. Sometimes, repeating decimals are indicated by a line over the digits that repeat. The number 3.7777 with 7 repeating, for instance, can also be written as 3.7. To convert a number like this to a fraction
you write it as an equation, multiply, subtract to remove the repeating decimal, and solve the equation.
Converting Basic Repeating Decimals
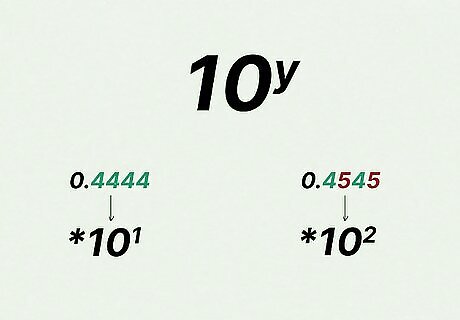
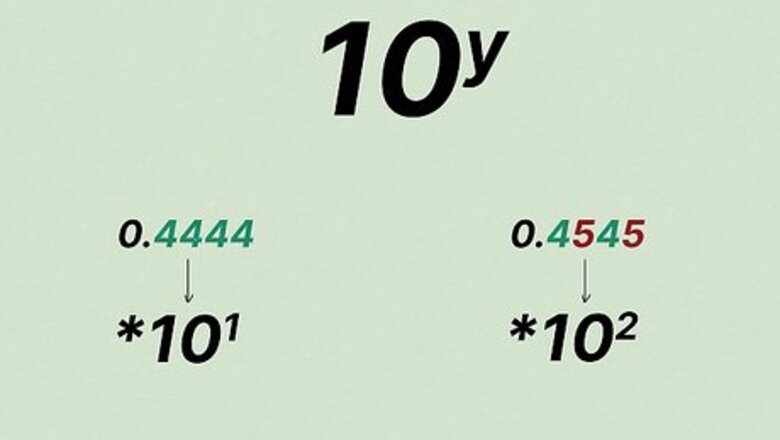
Locate the repeating decimal. For instance, the number 0.4444 has a repeating decimal of 4. It is a basic repeating decimal in the sense that there's no non-repeating portion to the decimal number. Count how many repeating digits there are in the pattern. Once your equation is written, you will multiply it by 10^y, where y equals the number of repeating digits in the pattern. In the example of 0.4444, there is one digit that repeats, so you will multiply the equation by 10^1. For a repeating decimal of 0.4545, there are two digits that repeat, and you would, therefore, multiply your equation by 10^2. For three repeating digits, multiply by 10^3, etc.

Rewrite the decimal as an equation. Write it out so that x equals the original number. In this instance, the equation is x = 0.4444. Since there’s only one digit in the repeating decimal, multiply the equation by 10^1 (which equals 10). In the example where x = 0.4444, then 10x = 4.4444. With the example x = 0.4545, there are two repeating digits, so you multiply both sides of the equation by 10^2 (which equals 100), giving you 100x = 45.4545.

Remove the repeating decimal. You accomplish this by subtracting x from 10x. Remember that whatever you do to one side of the equation must be done to the other, so: 10x – 1x = 4.4444 – 0.4444 On the left side, you have10x - 1x = 9x. On the right side, you have 4.4444 – 0.4444 = 4 Therefore, 9x = 4
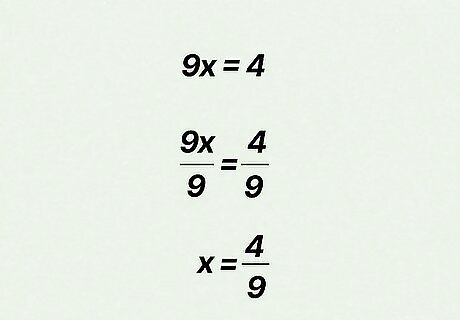
Solve for x. Once you know what 9x equals, you can determine what x equals by dividing both sides of the equation by 9: On the left side of the equation you have 9x ÷ 9 = x. On the right side of the equation you have 4/9 Therefore, x = 4/9, and the repeating decimal 0.4444 can be written as the fraction 4/9.

Reduce the fraction. Put the fraction in its simplest form (if applicable) by dividing both the numerator and denominator by the greatest common factor. In the example of 4/9, that is the simplest form. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher To simplify fractions, you can divide both the numerator and denominator by a common factor. This creates a new, easier-to-use fraction with smaller components, but it represents the same value. For instance, if you divide both the numerator and denominator of 6/12 by 2, you get 3/6, which is equal to 1/2.
Converting Numbers With Repeating and Non-Repeating Decimals
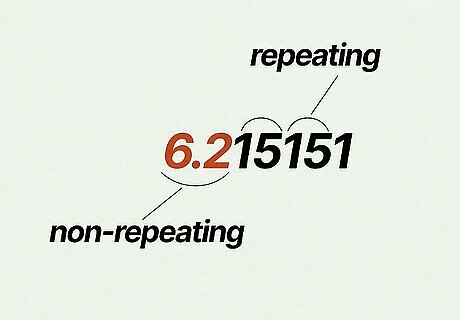
Determine the repeating digits. It’s not uncommon for a number to have non-repeating digits before the repeating decimal, but these can still be converted into fractions. For example, take the number 6.215151. Here, 6.2 is non-repeating, and the repeating digits are 15. Again take note of how many repeating digits there are in the pattern, because you will multiply by 10^y based on that number. In this example, there are two repeating digits, so you will multiply your equation by 10^2.

Write the problem as an equation and subtract the repeating decimals. Again, if x = 6.215151, then 100x = 621.5151. To remove the repeating decimals, subtract from both sides of the equation: 100x – x (= 99x) = 621.5151 - 6.215151 (= 615.3) Therefore, 99x = 615.3

Solve for x. Since 99x = 615.3, divide both sides of the equation by 99. This gives you x = 615.3/99.

Remove the decimal in the numerator. Do this by multiplying the numerator and denominator by 10^z, where z equals the number of decimal places you must move to eliminate the decimal. In 615.3, you have to move the decimal by one place, meaning you multiply the numerator and denominator by 10^1: 615.3 x 10 / 99 x 10 = 6153/990 Reduce the fraction by dividing the numerator and denominator by the highest common factor, which in this case is 3, giving you x = 2,051/ 330



















Comments
0 comment