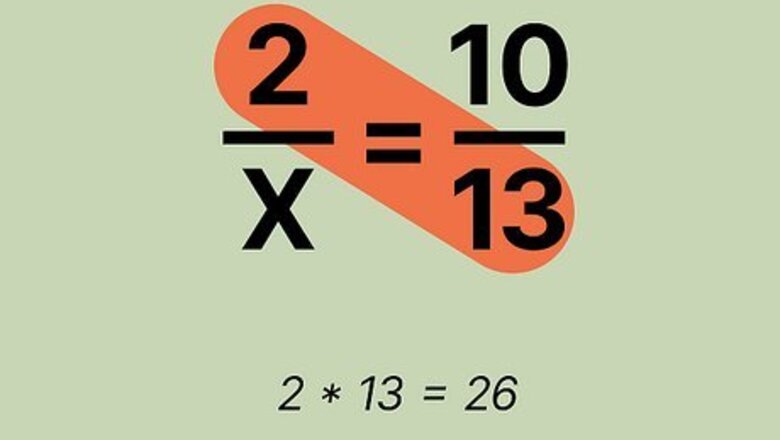
views
- Use the formula to cross-multiply the fractions in the equation
- Multiply the top number (numerator) of the fraction on the left side of the equal sign by the bottom number (denominator) of the fraction on the right side.
- Multiply the denominator of the left-hand fraction by the numerator of the right-hand fraction.
- Set the two products equal to one another and solve for the unknown variable.
Cross Multiplying with a Single Variable
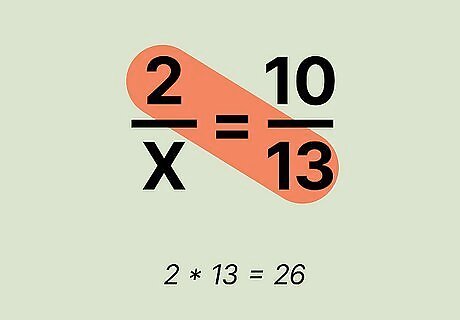
Multiply the numerator of the left fraction by the denominator of the right fraction. The numerator is the top number in a fraction, and the denominator is at the bottom. Let's say you're working with the equation 2 / x = 10 / 13 {\displaystyle 2/x=10/13} {\displaystyle 2/x=10/13}. You would then multiply the left numerator 2 by the right denominator 13. 2 x 13 = 26 {\displaystyle 2x13=26} {\displaystyle 2x13=26}.
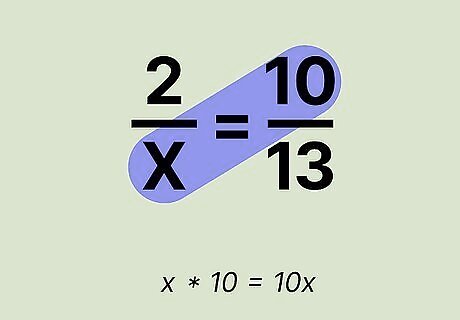
Multiply the numerator of the right fraction by the denominator of the left fraction. Now multiply 10 (the right numerator) by x (the left denominator). x x 10 = 10 x {\displaystyle xx10=10x} {\displaystyle xx10=10x}. It doesn’t really matter which pair of numerators and denominators you start multiplying first as long as you multiply both numerators by the denominators diagonal from them. Another way to think of cross-multiplication is by using this formula: if you have the equation a / b = c / d {\displaystyle a/b=c/d} {\displaystyle a/b=c/d}, you would multiply them out to get the equation a d = c b {\displaystyle ad=cb} {\displaystyle ad=cb}.
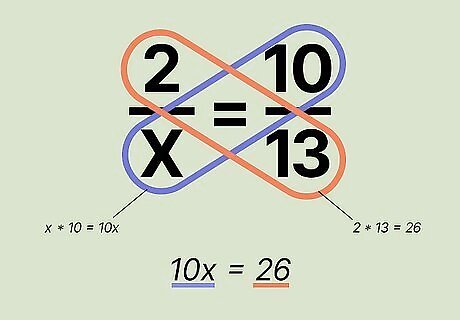
Set the two products equal to each other. Set 26 equal to 10x, written as 26 = 10 x {\displaystyle 26=10x} {\displaystyle 26=10x}. Since the two products are equal to one another, it doesn’t matter which number goes on which side. So both 26 = 10 x {\displaystyle 26=10x} {\displaystyle 26=10x} and 10 x = 26 {\displaystyle 10x=26} {\displaystyle 10x=26} are acceptable ways to write your equation.
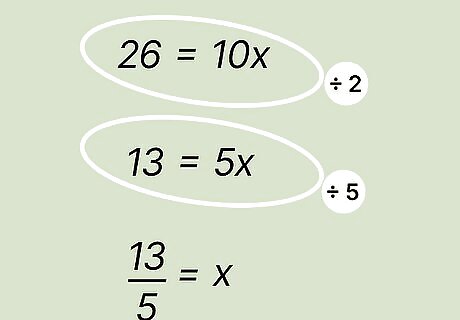
Solve for the variable x. Start by finding the greatest common factor between 26 and 10x. This is the largest number that divides exactly into both numbers. In this case, since both 26 and 10x are even numbers, they can both be divided by 2; 26 / 2 = 13 {\displaystyle 26/2=13} {\displaystyle 26/2=13} and 10 / 2 = 5 {\displaystyle 10/2=5} 10/2=5. You're left with 13 = 5 x {\displaystyle 13=5x} {\displaystyle 13=5x}. Then, to get x by itself and find its value, divide both sides of the equation by 5. So, 13 / 5 = 5 x / 5 {\displaystyle 13/5=5x/5} {\displaystyle 13/5=5x/5}, or 13 / 5 = x {\displaystyle 13/5=x} {\displaystyle 13/5=x}. If you'd like the convert the fraction to a decimal, start by dividing both sides of the equation by 10 to get 26 / 10 = 10 x / 10 {\displaystyle 26/10=10x/10} {\displaystyle 26/10=10x/10}, or 2.6 = x {\displaystyle 2.6=x} {\displaystyle 2.6=x}.
Cross Multiplying with Variables in Both Ratios
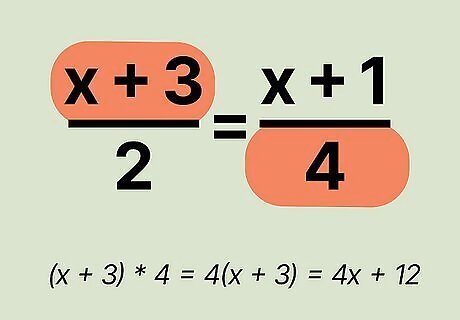
Multiply the numerator of the left ratio by the denominator of the right ratio. Let's say you're working with the following equation: ( x + 3 ) / 2 = ( x + 1 ) / 4 {\displaystyle (x+3)/2=(x+1)/4} {\displaystyle (x+3)/2=(x+1)/4}. Multiply (x + 3) by 4 to get 4 ( x + 3 ) {\displaystyle 4(x+3)} {\displaystyle 4(x+3)}. Then, distribute the 4 to get 4 x + 12 {\displaystyle 4x+12} {\displaystyle 4x+12}. To distribute the 4 into the equation (x + 3), multiply each part of the equation by 4. So that would be 4 x x + 4 x 3 = 4 x + 12 {\displaystyle 4xx+4x3=4x+12} {\displaystyle 4xx+4x3=4x+12}.
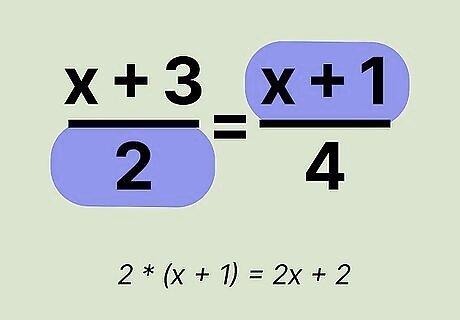
Multiply the numerator of the right ratio by the denominator of the left ratio. Repeat the process using the remaining numerator and denominator. ( x + 1 ) x 2 = 2 ( x + 1 ) {\displaystyle (x+1)x2=2(x+1)} {\displaystyle (x+1)x2=2(x+1)}. Distribute the 2 to get 2 x + 2 {\displaystyle 2x+2} {\displaystyle 2x+2}. ( 2 x x + 2 x 1 ) {\displaystyle (2xx+2x1)} {\displaystyle (2xx+2x1)}
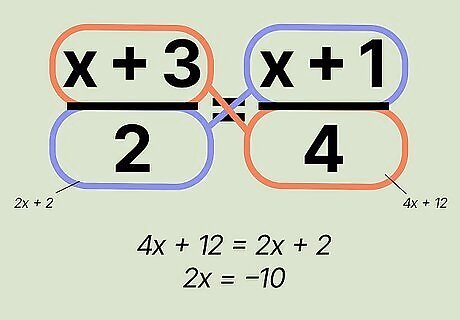
Set the two products equal to each other and combine the like terms. Now, you'll have 4 x + 12 = 2 x + 2 {\displaystyle 4x+12=2x+2} {\displaystyle 4x+12=2x+2}. Combine the x terms with each other on one side of the equation and the constants (the numbers without x) on the other side. Combine 4x and 2x by subtracting 2x from both sides. Subtracting 2x from 2x on the right side will leave you with 0. On the left side, 4 x − 2 x = 2 x {\displaystyle 4x-2x=2x} {\displaystyle 4x-2x=2x}, so 2x remains on the left-hand side of the equal sign. 2 x + 12 = 2 {\displaystyle 2x+12=2} {\displaystyle 2x+12=2} Then, combine 12 and 2 by subtracting 12 from both sides of the equation so that 2x is left by itself. Subtract 12 from 12 on the left to get 0, and subtract 12 from 2 on the right side to get -10 (since 2 − 12 = − 10 {\displaystyle 2-12=-10} {\displaystyle 2-12=-10}). You're left with 2 x = − 10 {\displaystyle 2x=-10} {\displaystyle 2x=-10}.
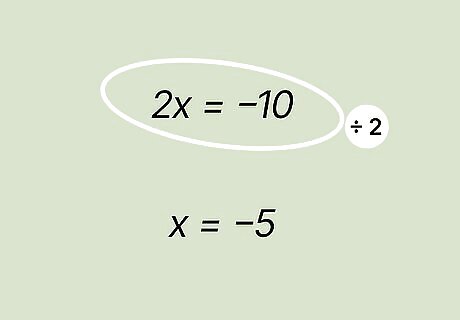
Solve for x by dividing each side by 2. This would be 2 x / 2 = − 10 / 2 {\displaystyle 2x/2=-10/2} {\displaystyle 2x/2=-10/2}, which yields x = − 5 {\displaystyle x=-5} x=-5. Go back and check your work by plugging in -5 for x in the original equation to make sure that both sides of the equation are equal. This would look like: ( − 5 + 3 ) / 2 = ( − 5 + 1 ) / 4 {\displaystyle (-5+3)/2=(-5+1)/4} {\displaystyle (-5+3)/2=(-5+1)/4}, which simplifies to − 1 = − 1 {\displaystyle -1=-1} {\displaystyle -1=-1}. Since this equation is true, it’s confirmed that x’s value is -5.

















Comments
0 comment