How to Find the Equation of a Perpendicular Line

Solving with One Point and an Equation

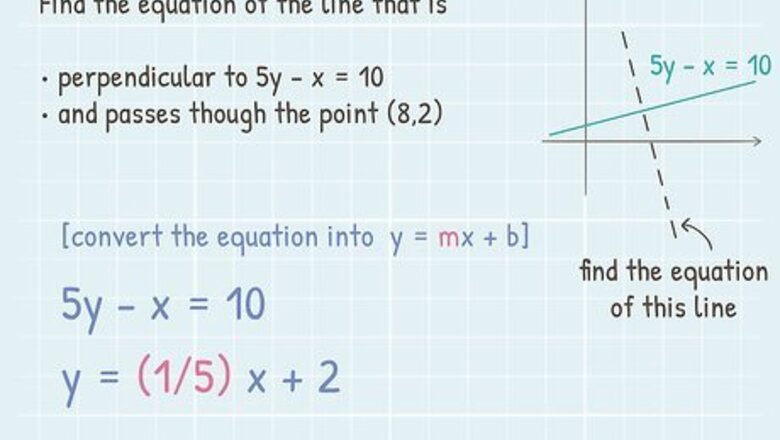
Simplify the equation of the line. If you are given the equation of a line and one common point and asked to find a line that runs perpendicular to it, it is important that you first convert the equation into the y = m x + b {\displaystyle y=mx+b} y=mx+b format. To do this, you want to get the y {\displaystyle y} y by itself. For example, say your given equation is 5 y − x = 10 {\displaystyle 5y-x=10} {\displaystyle 5y-x=10}. To isolate y {\displaystyle y} y, first move − x {\displaystyle {-x}} {\displaystyle {-x}} to the opposite side of the equation by adding it to both sides to get 5 y = x + 10 {\displaystyle 5y=x+10} {\displaystyle 5y=x+10} Get rid of the 5 {\displaystyle 5} 5 on the 5 y {\displaystyle 5y} {\displaystyle 5y} by dividing both sides of the equation by 5 {\displaystyle 5} 5. The new equation will be y = 1 5 x + 2 {\displaystyle y={\frac {1}{5}}x+2} {\displaystyle y={\frac {1}{5}}x+2}.

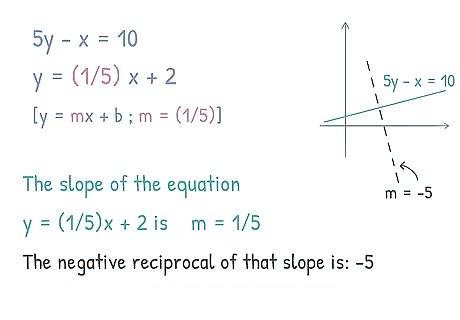
Calculate the opposite reciprocal of the slope. When a line is perpendicular to another line, the slope will be the negative opposite of the original line. This is called the opposite reciprocal. The lines cross each other at a right angle, so the slopes must be opposite. Two perpendicular slopes multiplied together will always equal − 1 {\displaystyle -1} -1. Remember that m {\displaystyle m} m represents the slope of the line. The opposite reciprocal of the equation y = 1 5 x + 2 {\displaystyle y={\frac {1}{5}}x+2} {\displaystyle y={\frac {1}{5}}x+2} would be − 5 1 x {\displaystyle {-}{\frac {5}{1}}x} {\displaystyle {-}{\frac {5}{1}}x} or − 5 {\displaystyle -5} -5.

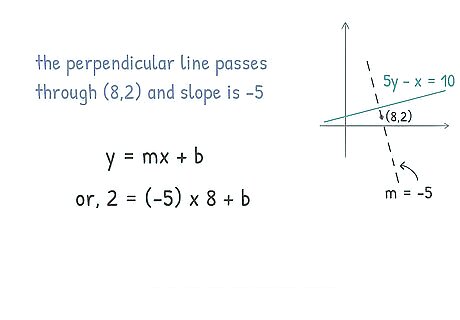
Plug the point into the slope equation to find the y-intercept. Now that you have the slope of the perpendicular line, you can plug the value of the slope and the point you were given into a slope equation. This will give you the value of the y-intercept. Using the y-intercept, you can move on to complete the slope equation. Remember that b {\displaystyle b} b represents the y-intercept of the line. For example, say your given point is ( 8 , 2 ) {\displaystyle (8,2)} {\displaystyle (8,2)} where 8 {\displaystyle 8} 8 represents the x {\displaystyle x} x coordinate and 2 {\displaystyle 2} {\displaystyle 2} is the y {\displaystyle y} y coordinate. Replace the letters in the y = m x + b {\displaystyle y=mx+b} y=mx+b equation with your known values of slope and xy coordinates: 2 = − 5 ( 8 ) + b {\displaystyle 2={-5}(8)+b} {\displaystyle 2={-5}(8)+b}

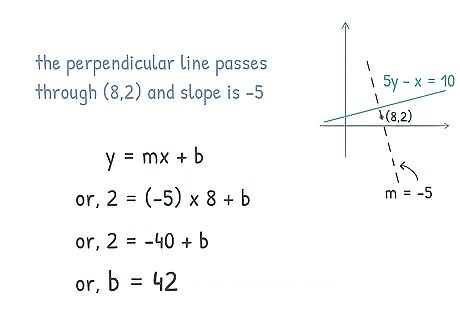
Solve the equation for the y-intercept. Once you have your values entered into the slope equation, it is time to isolate b {\displaystyle b} b, or the y-intercept. To isolate b {\displaystyle b} b, you must move all other numbers from one side of the equation. After you solve for the y-intercept, you will know all of the numbers needed to write the equation of the perpendicular line. To isolate b {\displaystyle b} b in the equation 2 = − 40 + b {\displaystyle 2={-40}+b} {\displaystyle 2={-40}+b}, add 40 {\displaystyle {40}} {\displaystyle {40}} to both sides. The equation for the y-intercept of the perpendicular line will be 42 = b {\displaystyle 42=b} {\displaystyle 42=b}

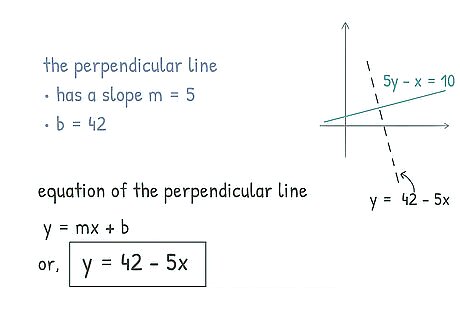
Use the values for slope and y-intercept to create your equation. Once you know the value for the slope and y-intercept of your line, all you have to do is reassemble the numbers into the slope formula y = m x + b {\displaystyle y=mx+b} y=mx+b. Substitute the m {\displaystyle m} m with the slope you have calculated and the b {\displaystyle b} b with the y-intercept you found. The formula for the perpendicular line would come out to be y = − 5 x + 42 {\displaystyle y={-5}x+42} {\displaystyle y={-5}x+42}

Calculating a Perpendicular Line Using Three Points

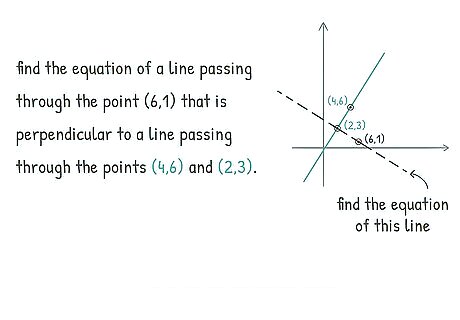
Understand the coordinates you were given. If you are given three coordinates from two perpendicular lines, they cannot all be used for the same equations. The first two coordinates will be used for one line, and the third will be used once you begin calculating the equation of the perpendicular line. The goal is finding two perpendicular y = m x + b {\displaystyle y=mx+b} y=mx+b equations. For example, you may be asked to find the coordinates of a line that passes through ( 6 , 1 ) {\displaystyle (6,1)} {\displaystyle (6,1)} based on a line that passes through ( 4 , 6 ) {\displaystyle (4,6)} {\displaystyle (4,6)} and ( 2 , 3 ) {\displaystyle (2,3)} {\displaystyle (2,3)}. Focus on ( 4 , 6 ) {\displaystyle (4,6)} {\displaystyle (4,6)} and ( 2 , 3 ) {\displaystyle (2,3)} {\displaystyle (2,3)} for now.

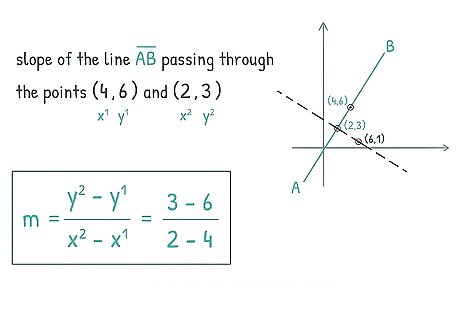
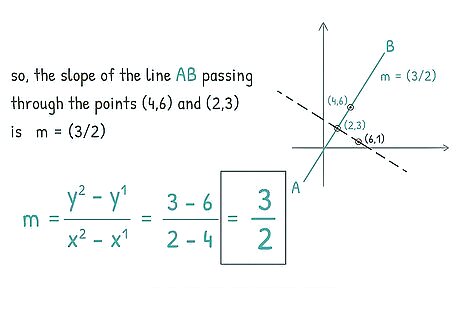
Substitute the points from the original line into the slope equation. You can use two separate points from one line to find the equation of a line that runs perpendicular to it. Before you calculate the equation of the perpendicular line, you will need to find the slope of the line that crosses the two points. The equation for finding the slope of a line with two points is m = y 2 − y 1 x 2 − x 1 {\displaystyle m={\frac {{y^{2}}-{y^{1}}}{{x^{2}}-{x^{1}}}}} {\displaystyle m={\frac {{y^{2}}-{y^{1}}}{{x^{2}}-{x^{1}}}}}. In this case, the numbers next to the x {\displaystyle x} x and y {\displaystyle y} y coordinates are not exponents, just a marker to show the different points. If your points are ( 4 , 6 ) {\displaystyle (4,6)} {\displaystyle (4,6)} and ( 2 , 3 ) {\displaystyle (2,3)} {\displaystyle (2,3)}, then the slope would be m = 3 − 6 2 − 4 {\displaystyle m={\frac {3-6}{2-4}}} {\displaystyle m={\frac {3-6}{2-4}}} m = 3 − 6 2 − 4 {\displaystyle m={\frac {3-6}{2-4}}} {\displaystyle m={\frac {3-6}{2-4}}} simplifies to − 3 − 2 {\displaystyle {\frac {-3}{-2}}} {\displaystyle {\frac {-3}{-2}}} which is equal to 3 2 {\displaystyle {\frac {3}{2}}} {\frac {3}{2}}. The slope of the line is 3 2 x {\displaystyle {\frac {3}{2}}x} {\displaystyle {\frac {3}{2}}x}

Combine the two points with the slope into an equation. Once you know the value of the slope m {\displaystyle m} m, you can use it to find the equation of your line by combining it with the x {\displaystyle x} x and y {\displaystyle y} y values. It does not matter which point you choose. The equation is y 2 − y 1 = m ( x 2 − x 1 ) {\displaystyle {y^{2}}-{y^{1}}=m({x^{2}}-{x^{1}})} {\displaystyle {y^{2}}-{y^{1}}=m({x^{2}}-{x^{1}})}. The exponents show the difference in the coordinates and do not represent any calculations. Using the points ( 4 , 6 ) {\displaystyle (4,6)} {\displaystyle (4,6)}, the equation would be y − 6 = 3 2 ∗ ( x − 4 ) {\displaystyle {y}-{6}={\frac {3}{2}}*({x}-4)} {\displaystyle {y}-{6}={\frac {3}{2}}*({x}-4)}.

Simplify the equation to solve for y {\displaystyle y} y. Once you have your chosen point and slope plugged into the equation, it is time to simplify. This will give you the equation of one line. After you know the equation of this line, you will be able to figure out the equation of the line that runs perpendicular to it. To simplify y − 6 = 3 2 ∗ ( x − 4 ) {\displaystyle {y}-{6}={\frac {3}{2}}*({x}-4)} {\displaystyle {y}-{6}={\frac {3}{2}}*({x}-4)}, first multiply all of the numbers in parentheses by the outer value to get y − 6 = 3 2 x − 6 {\displaystyle {y}-{6}={\frac {3}{2}}{x}-6} {\displaystyle {y}-{6}={\frac {3}{2}}{x}-6} Isolate the y {\displaystyle y} y on one side of the equation by adding 6 {\displaystyle 6} 6 to both sides to get y = 3 2 x + 0 {\displaystyle {y}={\frac {3}{2}}{x}+0} {\displaystyle {y}={\frac {3}{2}}{x}+0}. This is the equation of your first line.

Find the slope of the perpendicular line using the opposite reciprocal. A line perpendicular to another line will always have an opposite slope. If the slope of the original line is a positive whole number, then the slope of the perpendicular line will be a negative fraction. Two perpendicular slopes multiplied together will always equal − 1 {\displaystyle -1} -1. The opposite reciprocal of 3 2 x {\displaystyle {\frac {3}{2}}x} {\displaystyle {\frac {3}{2}}x} is − 2 3 x {\displaystyle {-}{\frac {2}{3}}x} {\displaystyle {-}{\frac {2}{3}}x}.

Solve the equation for the perpendicular line. Use the values for slope and the third point to find the equation of the perpendicular line. Now you know that the equation for the perpendicular line starts with y = − 2 3 x {\displaystyle y={-}{\frac {2}{3}}x} {\displaystyle y={-}{\frac {2}{3}}x}, but you still do not know what the y-intercept value is. By plugging your known point back into y 2 − y 1 = m ( x 2 − x 1 ) {\displaystyle {y^{2}}-{y^{1}}=m({x^{2}}-{x^{1}})} {\displaystyle {y^{2}}-{y^{1}}=m({x^{2}}-{x^{1}})} and adding the known value for m {\displaystyle m} m, you will get your answer. Using the coordinates from the perpendicular line ( 6 , 1 ) {\displaystyle (6,1)} {\displaystyle (6,1)} fill in the equation: y − 1 = − 2 3 ( x − 6 ) {\displaystyle {y}-{1}={-}{\frac {2}{3}}({x}-{6})} {\displaystyle {y}-{1}={-}{\frac {2}{3}}({x}-{6})}. Simplify the equation so that it reads y − 1 = − 2 3 x − 6 {\displaystyle y-{1}={-}{\frac {2}{3}}x-6} {\displaystyle y-{1}={-}{\frac {2}{3}}x-6} Isolate the y {\displaystyle y} y by adding 1 {\displaystyle 1} 1 to both sides. The equation now reads y = − 2 3 x − 5 {\displaystyle y={-}{\frac {2}{3}}x-5} {\displaystyle y={-}{\frac {2}{3}}x-5}. This is the final equation for the perpendicular line.