How to Make Sure a Corner is Square with the 3-4-5 Rule

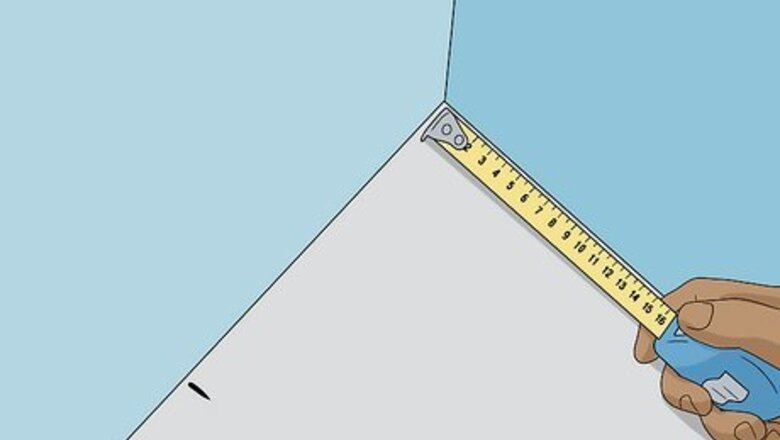
• Measure and mark 3 units from the corner along one side of your project, then measure and mark 4 units from the corner along the other side.
• Line up a tape measure between your marks and check to see if the length measures 5 units. If it does, the corner is square.
• The 3-4-5 rule uses the Pythagorean Theorem (A² + B² = C²) to ensure your corner forms a right triangle with a 90º angle.

Squaring a Corner with the 3-4-5 Method

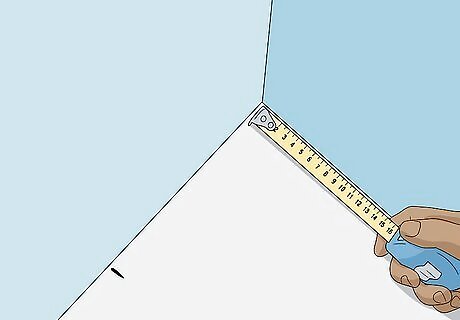
Measure 3 units from the corner along one side. Use a tape measure to measure 3 units out from the corner of your project, marking the measurement with a pencil. Use feet, meters, or any other unit to make your measurements, so long as you use the same unit each time.

Measure 4 units from the corner along the other side. Using the same unit of measurement, measure along the second side and make a mark at 4 units along its length. Multiply each number in the 3-4-5 rule by the same amount to scale it up for a larger project (to get a more accurate measurement), or to convert it to different units. For example, try 30-40-50 cm if you’re using the metric system. For a large room, use 6-8-10 or 9-12-15 feet or meters.

Measure the distance between your marks—if it's 5, your corner is square. Line up your tape measure between the 2 marks. If the distance is 5 units, your corner is square! If the distance is less than 5 units, your corner is less than 90º. If the distance is over 5 units, your corner has a measurement of more than 90º. Depending on your project, you may need to adjust your measurements or plans, or rebuild the corner to achieve a more precise angle. Use a framing square as a guide when you do this to avoid further mistakes. Once you’ve got a square corner, check the project’s other 3 corners to ensure they’re the same.

Why does the 3-4-5 rule work?

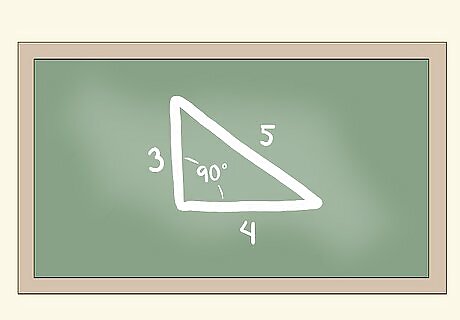
The 3-4-5 rule uses the Pythagorean Theorem to make a right angle. If a triangle has sides measuring 3, 4, and 5 units long, it must be a right triangle with a 90º angle between the short sides. If you can "find" this triangle in your corner, you know the corner is square. This is based on the Pythagorean Theorem from geometry: A + B = C for a right triangle. C is the longest side (hypotenuse) and A and B are the two shorter "legs." 3-4-5 is a very convenient measurement to check because of the low, whole numbers. The math checks out: 3 + 4 = 9 + 16 = 25 = 5. The 3-4-5 rule works with any numbers of the same proportions. For example, finding a triangle with sides that are 6-8-10 or 9-12-15 units long will also give you a 90º angle. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Use this visual trick to understand the Pythagorean Theorem. Imagine a right triangle with squares constructed on each leg and the hypotenuse. by rearranging the smaller squares within the larger square, the areas of the smaller squares (a² and b²) will add up visually to the area of the larger square (c²).