
views
See if the equation equals zero.

If it does, the equation is ready for you to solve. You can't use quadratic formula until the equation equals 0 {\displaystyle 0} {\displaystyle 0}. If the equation you’re looking at doesn’t equal zero, don’t worry. We'll show you how to convert it. Here's a quadratic equation in standard form: a x 2 {\displaystyle ax^{2}} {\displaystyle ax^{2}} + b x + c = 0 {\displaystyle +bx+c=0} {\displaystyle +bx+c=0} Here are 2 examples to demonstrate: x 2 − 3 x + 1 = 0 {\displaystyle x^{2}-3x+1=0} {\displaystyle x^{2}-3x+1=0}This equation is ready to solve because it equals 0 {\displaystyle 0} {\displaystyle 0}. − 3 x 2 + 6 x = − 5 {\displaystyle -3x^{2}+6x=-5} {\displaystyle -3x^{2}+6x=-5}This equation is not ready to solve just yet. We need to convert it first.
Convert the equation to standard form.
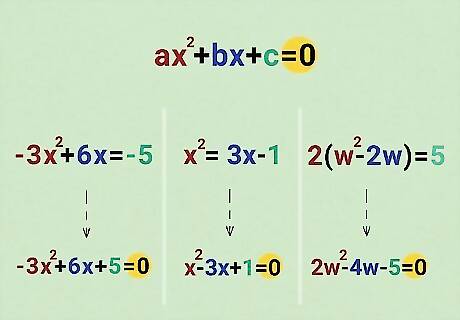
Standard form means the equation equals “0” and is ready to solve. It might sound complicated, but converting to standard form is pretty easy. You just need to move some things around a bit! It’s easier to show you, so check out these examples: If an equation looks like this: − 3 x 2 + 6 x = − 5 {\displaystyle -3x^{2}+6x=-5} {\displaystyle -3x^{2}+6x=-5} Move the − 5 {\displaystyle -5} -5 to the left side of the equal sign and put 0 {\displaystyle 0} {\displaystyle 0} on the right side of the equal sign. Remember: numerals change from + {\displaystyle +} + to − {\displaystyle -} - (or vice versa) when you move them to the other side of the equal sign. Our converted equation: − 3 x 2 + 6 x + 5 = 0 {\displaystyle -3x^{2}+6x+5=0} {\displaystyle -3x^{2}+6x+5=0} If an equation looks like this: x 2 = 3 x − 1 {\displaystyle x^{2}=3x-1} {\displaystyle x^{2}=3x-1} Move all the terms to left side of the equal sign. Our converted equation: x 2 − 3 x + 1 = 0 {\displaystyle x^{2}-3x+1=0} {\displaystyle x^{2}-3x+1=0} If an equation looks like this: 2 ( w 2 − 2 w ) = 5 {\displaystyle 2(w^{2}-2w)=5} {\displaystyle 2(w^{2}-2w)=5} Undo the brackets to expand and move 5 to the left of the equal sign. Our converted equation: 2 w 2 − 4 w − 5 = 0 {\displaystyle 2w^{2}-4w-5=0} {\displaystyle 2w^{2}-4w-5=0}
Identify the coefficients.
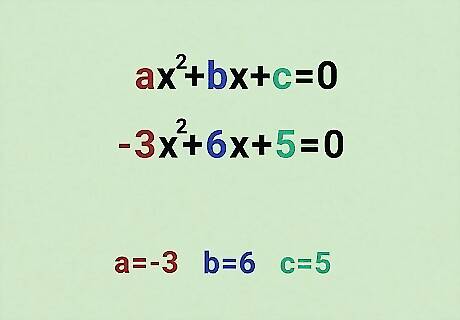
The coefficients are the a, b, and c in the standard form equation. Remember, the standard formula is a x 2 {\displaystyle ax^{2}} {\displaystyle ax^{2}} + b x + c = 0 {\displaystyle +bx+c=0} {\displaystyle +bx+c=0}. Our equation in standard formula is − 3 x 2 + 6 x + 5 = 0 {\displaystyle -3x^{2}+6x+5=0} {\displaystyle -3x^{2}+6x+5=0}. All you have to figure out a, b, and c. The coefficients in our equation: a = − 3 {\displaystyle a=-3} {\displaystyle a=-3} b = 6 {\displaystyle b=6} b=6 c = 5 {\displaystyle c=5} {\displaystyle c=5}
Plug the coefficients into the quadratic formula.
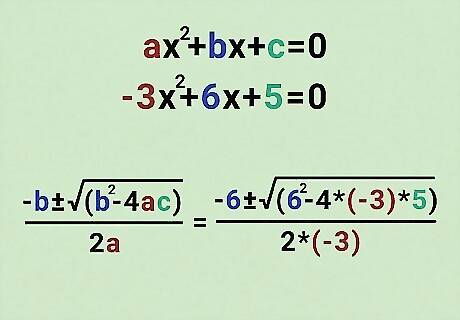
Replace the a, b, and c in the quadratic formula with our coefficients. This part is easy! Just switch out the letters with the coefficients. Remember, the quadratic formula looks like this: x = − b {\displaystyle x=-b} {\displaystyle x=-b}± √( b 2 − 4 a c ) {\displaystyle b^{2}-4ac)} {\displaystyle b^{2}-4ac)} / 2 a {\displaystyle /2a} {\displaystyle /2a} Our coefficients: a = − 3 {\displaystyle a=-3} {\displaystyle a=-3}, b = 6 {\displaystyle b=6} b=6, and c = 5 {\displaystyle c=5} {\displaystyle c=5} Our equation after inserting the coefficients: x = − 6 {\displaystyle x=-6} x = -6± √( 6 2 − ( 4 ) ( − 3 ) ( 5 ) {\displaystyle 6^{2}-(4)(-3)(5)} {\displaystyle 6^{2}-(4)(-3)(5)} / 2 ( − 3 ) {\displaystyle /2(-3)} {\displaystyle /2(-3)}
Use the order of operations to simplify the formula.
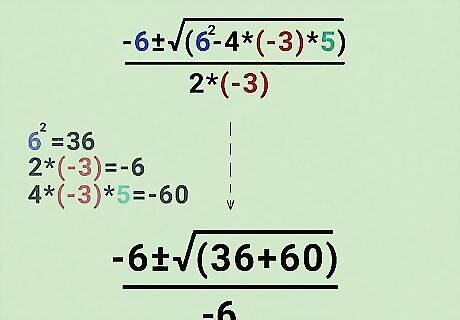
Just do the math in the equation as you normally would. Now that all the coefficients have a numerical value, you can do the simple math in the equation. 6 2 = 36 {\displaystyle 6^{2}=36} 6^{2}=36 2 {\displaystyle 2} {\displaystyle 2} x − 3 = − 6 {\displaystyle -3=-6} {\displaystyle -3=-6} − 3 {\displaystyle -3} -3 x 5 = − 15 {\displaystyle 5=-15} {\displaystyle 5=-15} − 15 {\displaystyle -15} {\displaystyle -15} x − 4 {\displaystyle -4} -4 = 60 {\displaystyle 60} 60 You end up with: x = − 6 {\displaystyle x=-6} {\displaystyle x=-6}± √ ( 36 + 60 ) {\displaystyle (36+60)} {\displaystyle (36+60)} / − 6 {\displaystyle /-6} {\displaystyle /-6} Then, simplify once more: x = − 6 {\displaystyle x=-6} x = -6± √ 96 {\displaystyle 96} {\displaystyle 96} / − 6 {\displaystyle /-6} {\displaystyle /-6}
Simplify the radical.
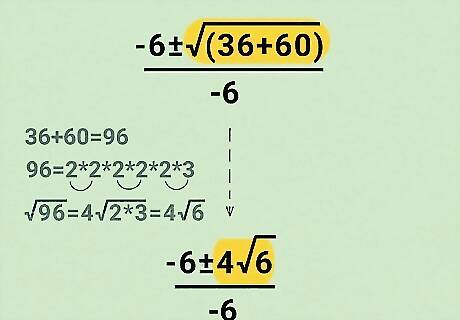
The radical is the number inside √ which is 96. To simplify, find the prime factorization of the number inside the radical. "Prime factorization" means dividing the number by 2 (the first prime number). Then, continue dividing by 2 until you get a decimal or remainder. At that point, divide by 3, 5, 7, etc. until all you have left are prime numbers. Here's the prime factorization of 96: 2 x 2 x 2 x 2 x 2 x 3 = 96. Group the pairs: (2 x 2) (2 x 2). There are four 2s, so 4 goes outside the radical sign. Multiply what's left: (2 x 3) = 6. This goes inside the radical sign. So √ 96 {\displaystyle 96} {\displaystyle 96} simplified = 4√ 6 {\displaystyle 6} 6 Putting it all together: x = − 6 {\displaystyle x=-6} x = -6± 4√ 6 {\displaystyle 6} 6 / − 6 {\displaystyle /-6} {\displaystyle /-6}
Reduce the problem.
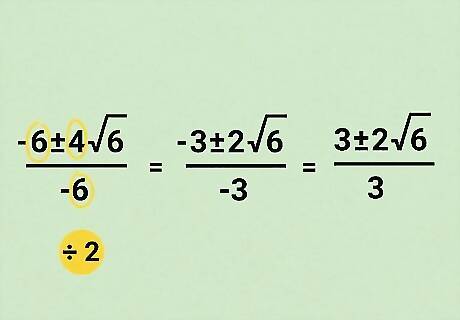
Our equation can be reduced by 2. -6, 4, and 6 are all divisible by 2. That means the equation can be reduced by 2. Divide each number by 2: -6 ÷ 2 = -3 4 ÷ 2 = 2 6 ÷ 2 = 3 The reduced equation: x = − 3 {\displaystyle x=-3} x=-3± 2√ 6 {\displaystyle 6} 6 / − 3 {\displaystyle /-3} {\displaystyle /-3} or x = 3 {\displaystyle x=3} x=3± 2√ 6 {\displaystyle 6} {\displaystyle 6} / 3 {\displaystyle /3} {\displaystyle /3}(both answers are correct because of the ± sign) These are your final answers.
Circle your answer(s).
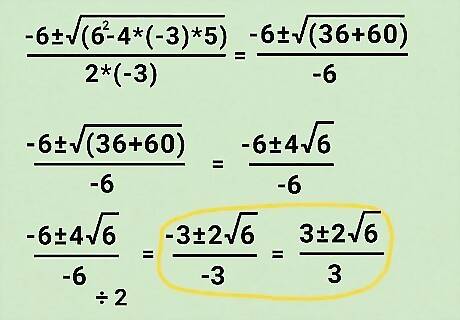
It'll make it easier for your teacher grade your work. You just did a lot of math there! Most teachers want you to "show your work," which means your teacher is going to see all of that. Go ahead and circle your answer so it'll stand out from the rest of the work on the page.
Memorize the quadratic formula.
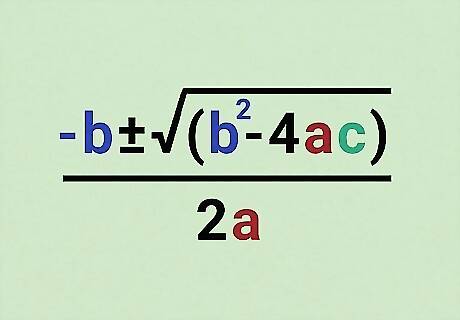
The quadratic formula is x = − b {\displaystyle x=-b} {\displaystyle x=-b}± √( b 2 − 4 a c ) {\displaystyle b^{2}-4ac)} {\displaystyle b^{2}-4ac)} / 2 a {\displaystyle /2a} {\displaystyle /2a}. You'll need to memorize the formula at some point (probably for the upcoming exam), so committing it to memory now isn't a bad idea. The formula might look a bit complicated at first glance, but we have some fun tips to help you out. Sing these lyrics to the tune of Pop Goes the Weasel:X is equal to negative BPlus or minus the square rootOf B-squared minus four A CAll over two A If songs aren't your thing, try memorizing this story instead:A negative boy was thinking yes or no about going to a party.At the party, he talked to a square boy but not to the 4 awesome cats.It was all over at 2 am.

















Comments
0 comment