Is Zero a Positive or Negative Integer? Here’s the Surprising Answer

Alleres

Editor

posted on 1 year ago — updated on 1 second ago

30
views

If you’re taking a math class, you’ll definitely encounter integers, as well as positive and negative numbers. But where does 0 fall within these categories? Is it positive or negative? Is it an integer or not? If these questions have you scratching your head, you’re not alone. 0 is an oddball in math, and categorizing it requires some extra thinking and creativity. This guide will help you understand exactly how 0 fits in with respect to positive and negative integers. Keep reading for a crystal clear explanation, plus a few examples to really bring these ideas home.

Things You Should Know

Zero is an integer, but it’s neither positive nor negative. It’s the only number that’s not positive or negative.
Zero is neither greater than zero nor less than zero. Therefore, by this definition, it’s neither positive nor negative.
Zero is still an integer because it’s a whole number and doesn’t contain any fractional part. This means it contains no fractions or decimals.
A positive integer is a whole number greater than zero, while a negative integer is a whole number less than zero.

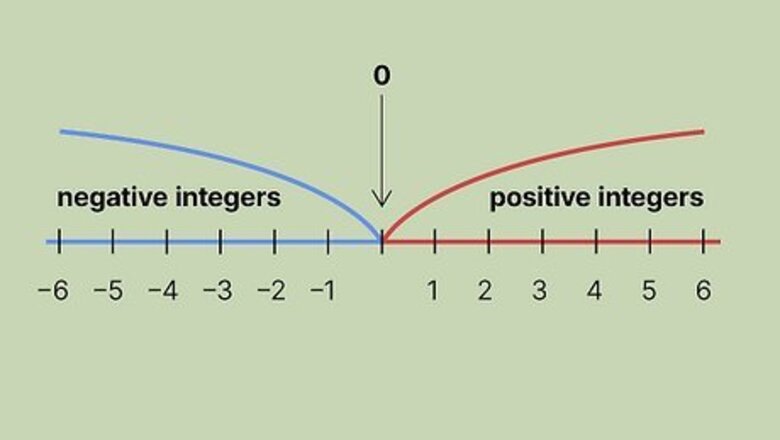
Is zero a positive or negative integer?

Zero is an integer, but it's neither positive nor negative. On a traditional number line, zero sits in the middle between the positive and negative numbers. By definition, negative numbers are less than zero and located to the left of zero on a number line, while positive numbers are greater than zero and located to the right. Since zero doesn’t fit these definitions, it’s not considered positive or negative. Zero is the only number that isn’t positive or negative.

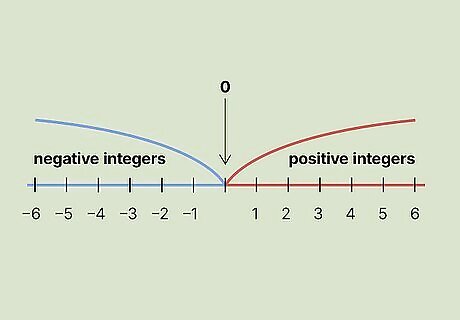
Why is 0 an integer?

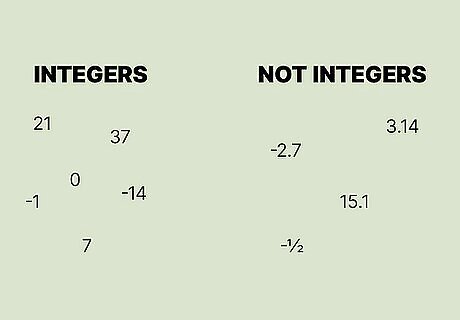
0 is an integer because it is a whole number. A “whole” number is any number that has no fractional parts. In other words, it doesn’t contain fractions or decimals. An integer can be positive, negative, or 0, but it cannot have fractional parts. For example, the numbers -14, -1, 0, 7, 21, and 37 are all integers because they are whole numbers. The numbers -2.7, -½, 15.1, and π are not integers because they contain fractional parts (either as fractions or decimals).

Proof that Zero Can’t be Positive or Negative

If 0 was positive, it would break the rules of multiplying negative numbers. Let’s use the example -2 x 0 = 0, assuming zero is positive. We know that -2 is a negative number. We also know that if we multiply a negative number by a positive number, the answer will always be negative. Therefore, if we assume 0 is positive, then -2 x 0 should give us a negative answer. But the answer is 0, which we said was positive. This is a contradiction, which means our original assumption was incorrect. Since a number can’t be positive and negative at the same time, we must assume that 0 is neither positive nor negative.

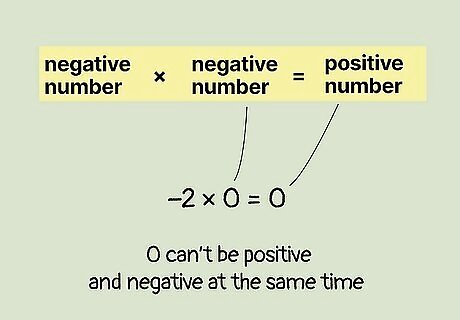
If 0 was negative, it’d also break the rules of multiplying negative numbers. Let’s try -2 x 0 = 0 again, assuming zero is negative this time. We know that -2 is a negative number. We also know that if we multiply a negative number by another negative number, the answer will always be positive. Therefore, if we assume 0 is negative, then -2 x 0 should give us a positive answer. But the answer is 0, which we assumed was negative. Once again, we have a contradiction. This proves that our original assumption was wrong. A number can’t be negative and positive at the same time. Therefore, 0 is neither positive nor negative.